Zadanie nr 1493212
Wykonano następującą konstrukcję.
1. Narysowano romb 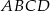 .
.
2. Wykreślono przekątne rombu i ich punkt przecięcia oznaczono literą 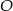 .
.
3. Poprowadzono prostą prostopadłą do boku 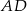 i przechodzącą przez punkt
i przechodzącą przez punkt 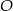 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 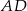 oznaczono literą
oznaczono literą 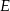 .
.
4. Narysowano okrąg o środku w punkcie 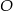 i promieniu
i promieniu 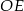 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego rombu.
B) jest styczny do wszystkich boków tego rombu.
C) jest styczny do przekątnych tego rombu.
D) nie ma punktów wspólnych z jednym z boków rombu.
Rozwiązanie
Szkicujemy opisaną konstrukcję
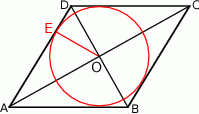
Widać, że skonstruowaliśmy okrąg wpisany w romb.
Odpowiedź: B

