/Szkoła podstawowa/Zadania testowe/Geometria/Romb

Zadanie nr 9268309

Na rysunku przedstawiono romb i jego przekątne. Długości odcinków na jakie dzielą się przekątne tego rombu są opisane za pomocą wyrażeń.

PIC

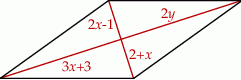
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

Obwód rombu jest równy 52.PF
Pole rombu jest równe 240. PF
Wersja PDF

Rozwiązanie

Ponieważ przekątne rombu dzielą się na połowy, to mamy

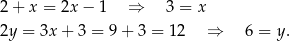
2 + x = 2x − 1 ⇒ 3 = x 2y = 3x+ 3 = 9 + 3 = 12 ⇒ 6 = y.

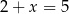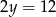Przekątne rombu mają więc długości 2+ x = 5 i 2y = 12 . Pole jednego z czterech trójkątów prostokątnych, z których zbudowany jest romb jest równe

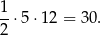
1 --⋅5 ⋅12 = 30 . 2

Pole rombu jest więc równe

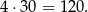
4⋅ 30 = 120.

Bok a rombu obliczamy z twierdzenia Pitagorasa (przekątne rombu są prostopadłe).

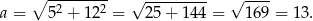
∘ --------- a = 52 + 122 = √ 25-+-1-44 = √ 169-= 13.

Obwód rombu jest więc równy 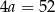4a = 52 .  
Odpowiedź: P, F

Wersja PDF