Zadanie nr 3306780
Pan Kowalski zaciągnął w banku kredyt w wysokości 40000 zł. Oprocentowanie kredytu wynosi 12% w skali roku, a odsetki są dopisywane kwartalnie. Kredyt ma zostać spłacony w czterech równych ratach kwartalnych (spłacanych na koniec każdego kwartału). Wyznacz wysokość raty.
Rozwiązanie
Sposób I
Oznaczmy szukaną wysokość każdej z rat przez  . W takim razie po pierwszym kwartale zadłużenie Pana Kowalskiego wynosi
. W takim razie po pierwszym kwartale zadłużenie Pana Kowalskiego wynosi
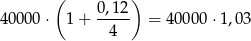
i  złotych z tej kwoty zostaje spłacone.
złotych z tej kwoty zostaje spłacone.
Po drugim kwartale zadłużenie wynosi
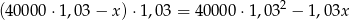
i znowu  z tej kwoty zostanie spłacone.
z tej kwoty zostanie spłacone.
Po trzecim kwartale zadłużenie wynosi
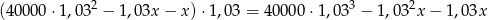
i znowu  z tej kwoty zostanie spłacone.
z tej kwoty zostanie spłacone.
Wreszcie na koniec roku pozostanie zadłużenie
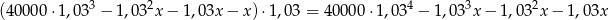
i musi być równe wysokości ostatniej raty. Daje to nam równanie
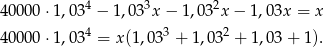
Możemy obie strony policzyć na kalkulatorze, ale możemy też zauważyć, że w nawiasie mamy kolejne wyrazy ciągu geometrycznego, czyli
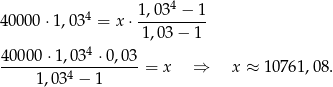
Sposób II
Jak poprzednio, niech  będzie szukaną wysokością raty. Tym razem będziemy jednak liczyć jaką część wyjściowej kwoty kredytu spłacamy w kolejnych ratach.
będzie szukaną wysokością raty. Tym razem będziemy jednak liczyć jaką część wyjściowej kwoty kredytu spłacamy w kolejnych ratach.
W pierwszej racie spłacamy  złotych, ale ponieważ zostały dopisane odsetki w wysokości
złotych, ale ponieważ zostały dopisane odsetki w wysokości 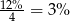 więc to
więc to  złotych spłaca tylko
złotych spłaca tylko
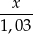
oryginalnego zadłużenia (jak pomnożymy tę liczbę przez przyrost odsetek 1,03 to otrzymamy ratę w wysokości  ).
).
Podobnie w drugiej racie, spłacamy tylko
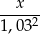
oryginalnego zadłużenia (bo kwota, którą spłacamy po kapitalizacji, czyli pomnożeniu przez 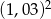 , ma dać
, ma dać  ). W trzeciej i czwartej racie spłacamy odpowiednio
). W trzeciej i czwartej racie spłacamy odpowiednio 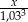 i
i 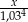 pierwotnego zadłużenia.
pierwotnego zadłużenia.
W sumie mamy do spłacenia 40000 zł, co daje nam równanie
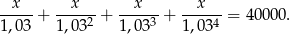
Jak w poprzednim sposobie zauważamy, że z lewej strony mamy sumę kolejnych wyrazów ciągu geometrycznego, czyli
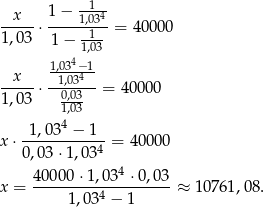
Odpowiedź: 10761,08 zł

