/Szkoła średnia/Zadania z treścią/Procenty

Zadanie nr 3469181

Dodaj do ulubionych
Dodaj do rozwiązanych

W 1995 roku pan Nowak wpłacił 10000zł na dwuletnią lokatę z roczną kapitalizacją odsetek. Po roku bank obniżył roczną stopę procentową o dwa punkty procentowe. Po dwóch latach pan Nowak wypłacił całą kwotę, która wraz z odsetkami wyniosła 16640zł. Oblicz, jakie było oprocentowanie lokaty w pierwszym roku, a jakie w drugim (w latach 90-tych nie było podatku od odsetek).

Rozwiązanie

Oznaczmy oprocentowanie lokaty w pierwszym roku przez 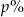p% . Po pierwszym roku pan Nowak miał na lokacie

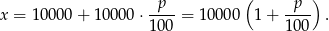
p ( p ) x = 10000 + 1 0000 ⋅----= 10000 1 + ---- . 100 1 00

W drugim roku dopisano do tej kwoty 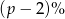(p − 2)% odsetek. Mamy więc równanie

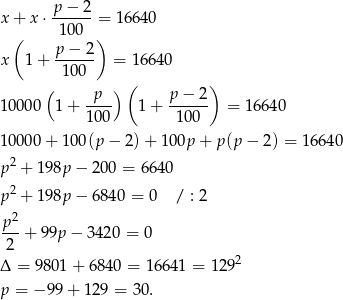
p− 2 x + x⋅ ------= 16 640 ( 100 ) x 1+ p-−-2- = 1 6640 100 ( ) ( ) 1 0000 1 + -p-- 1 + p−--2- = 1664 0 100 1 00 1 0000 + 100(p − 2)+ 1 00p + p(p − 2 ) = 16640 p 2 + 198p − 200 = 6640 2 p + 198p − 684 0 = 0 / : 2 p2 ---+ 99p − 3 420 = 0 2 2 Δ = 98 01+ 6840 = 1 6641 = 12 9 p = − 99 + 129 = 30.

 
Odpowiedź: 30% i 28%

Wersja PDF