Zadanie nr 5450303
Mamy trzy roztwory, każdy zawierający chlorek sodu i chlorek potasu. Procentową zawartość obu chlorków w roztworach podano w tabeli.
| Roztwór | NaCl (chlorek sodu) | KCl (chlorek potasu) |
| I | 14,1% | 2,5% |
| II | 8,7% | 8,2% |
| III | 1,5% | 5,7% |
W jakim stosunku należy zmieszać wszystkie trzy roztwory, aby otrzymać roztwór, w którym stężenie każdego z chlorków wynosić będzie 6%?
Rozwiązanie
Jasne jest, że istotne są tylko proporcje w jakich zmieszamy dane roztwory, a nie ich dokładne ilości. Powiedzmy, że pierwszego roztworu weźmiemy 1 (litr), drugiego  , a trzeciego
, a trzeciego 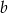 . Policzmy ile będzie czystego chlorku sodu i chlorku potasu w otrzymanym roztworze.
. Policzmy ile będzie czystego chlorku sodu i chlorku potasu w otrzymanym roztworze.
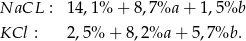
Mamy zatem układ równań
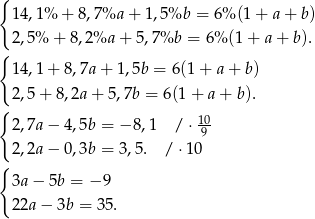
Pozostało rozwiązać ten układ równań.
Sposób I
Stosujemy metodą wyznacznikową.
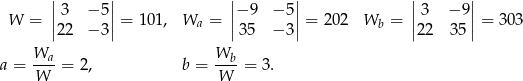
Sposób II
Mnożymy pierwsze równanie przez 3, a drugie przez 5 i odejmujemy je stronami (żeby zredukować 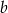 ). Mamy zatem
). Mamy zatem
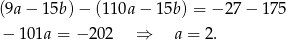
Stąd
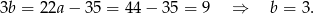
Odpowiedź: 1:2:3

