Zadanie nr 9376905
Wyprowadź wzór 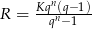 na wysokość raty
na wysokość raty 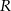 kredytu udzielonego w kwocie
kredytu udzielonego w kwocie 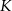 , przy założeniu, że:
, przy założeniu, że:
– spłata tego kredytu jest rozłożona na  równych rat płaconych miesięcznie;
równych rat płaconych miesięcznie;
– pierwszą ratę wpłacamy po miesiącu od daty udzielenia kredytu;
– roczne oprocentowanie kredytu jest równe  i
i 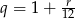 .
.
Rozwiązanie
Cała trudność w ustaleniu wysokości raty kredytu polega na tym, że spłacając kredyt zmniejszamy kwotę, od której są naliczane odsetki, więc w każdej racie stosunek wartości odsetek do spłacanego kapitału jest inny (dokładniej: robi się coraz mniejszy).
Aby łatwo ominąć ten problem zastosujemy podstawową zasadę matematyki finansowej: spróbujemy wszystkie raty i zobowiązania sprowadzić do jednego punktu w czasie – powiedzmy do momentu spłaty kredytu (czyli daty płatności ostatniej raty).
Zauważmy najpierw, że jeżeli wpłacamy do banku 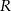 złotych, to po jednym miesiącu wartość tych pieniędzy urośnie do
złotych, to po jednym miesiącu wartość tych pieniędzy urośnie do
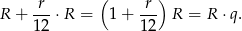
Po kolejnym miesiącu wartość wzrośnie do
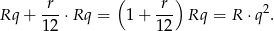
itd. W takim razie w momencie wpłaty ostatniej raty kredytu wpłacone przez nas raty będą miały wartość (liczymy od końca, czyli od ostatniej wpłaconej raty)
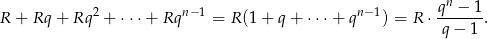
Z drugiej strony nasze zobowiązanie zaciągnięte od banku będzie w tym momencie miało wartość
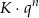
(przesuwamy to zobowiązanie o  okresów w przyszłość). Mamy więc równanie
okresów w przyszłość). Mamy więc równanie