Zadanie nr 2059831
Dany jest okrąg o środku 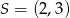 i promieniu
i promieniu 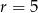 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 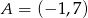 B)
B) 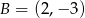 C)
C) 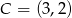 D)
D) 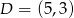
Rozwiązanie
Sposób I
Musimy sprawdzić, dla którego z podanych punktów odległość od 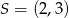 jest równa 5. Sprawdzamy kolejno
jest równa 5. Sprawdzamy kolejno
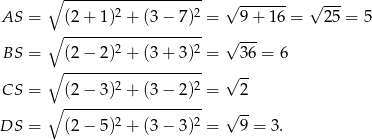
Sposób II
Równanie okręgu, o którym mowa to
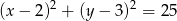
i pozostało sprawdzić, który z podanych punktów je spełnia. Gdy to zrobimy, okaże się, że jest to punkt 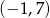 .
.
Odpowiedź: A

