/Szkoła średnia/Równania/Wymierne

Zadanie nr 2004036

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 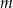m suma odwrotności pierwiastków równania

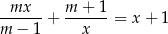
--mx-- + m--+-1 = x+ 1 m − 1 x

jest nie większa od 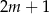2m + 1 ?

Rozwiązanie

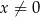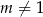Oczywiście musi być x ⁄= 0 i m ⁄= 1 . Przy tych założeniach równanie może przekształcić do zwykłego równania kwadratowego.

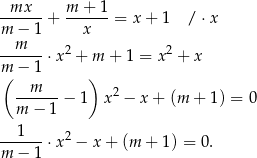
--mx-- + m--+-1 = x+ 1 / ⋅x m − 1 x --m--- ⋅x2 + m + 1 = x2 + x m − 1 ( m ) ------− 1 x2 − x+ (m + 1) = 0 m − 1 ---1-- 2 m − 1 ⋅x − x + (m + 1) = 0.

Równanie ma mieć pierwiastki, więc musi być

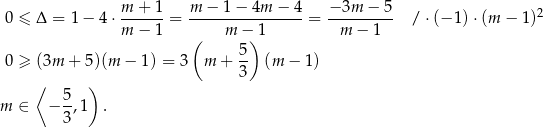
m--+-1 m-−--1−-4m--−-4- −-3m-−--5 2 0 ≤ Δ = 1− 4⋅m − 1 = m − 1 = m − 1 / ⋅(− 1) ⋅(m − 1) ( 5) 0 ≥ (3m + 5)(m − 1) = 3 m + -- (m − 1) ⟨ ) 3 5 m ∈ − --,1 . 3

Sprawdźmy jeszcze co się dzieje, gdy równanie ma jedno rozwiązanie, czyli gdy 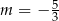m = − 5 3 . Mamy wtedy równanie kwadratowe

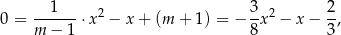
--1--- 2 3-2 2- 0 = m − 1 ⋅x − x+ (m + 1 ) = − 8x − x − 3 ,

którego jedynym pierwiastkiem jest 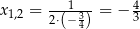---1-- 4 x1,2 = 2⋅(−34) = − 3 . Z drugiej strony, wtedy 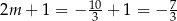2m + 1 = − 10 + 1 = − 7 3 3 i łatwo sprawdzić, że nierówność

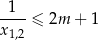
-1-- x ≤ 2m + 1 1,2

nie jest spełniona.

Zauważmy jeszcze, że 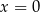x = 0 jest pierwiastkiem powyższego równania kwadratowego wtedy i tylko wtedy, gdy 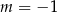m = − 1 i mamy wtedy równanie

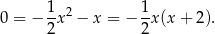
1 1 0 = − -x2 − x = − --x(x + 2). 2 2

Wyjściowe równanie ma więc w tym przypadku jedno rozwiązanie 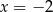x = − 2 i łatwo sprawdzić, że nie jest spełniona nierówność

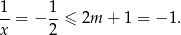
1-= − 1-≤ 2m + 1 = − 1. x 2

Pozostało zająć się sytuacją, gdy dane równanie ma dwa niezerowe pierwiastki 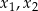x1,x 2 . Na mocy wzorów Viète’a mamy wtedy

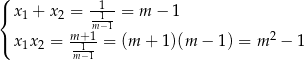
( 1 { x1 + x2 = --1-= m − 1 m-+m1 −1 2 ( x1x2 = m1−1 = (m + 1)(m − 1) = m − 1

i musimy rozwiązać nierówność

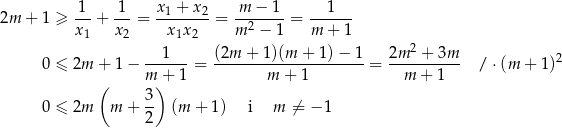
-1- 1-- x-1 +-x-2 -m-−-1- --1--- 2m + 1 ≥ x1 + x2 = x1x2 = m 2 − 1 = m + 1 2 0 ≤ 2m + 1− --1---= (2m--+-1)(m-+--1)−--1 = 2m---+-3m- / ⋅(m + 1)2 ( m)+ 1 m + 1 m + 1 3 0 ≤ 2m m + -- (m + 1) i m ⁄= −1 2

Rozwiązaniem tej nierówności jest zbiór

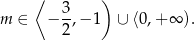
⟨ ) 3- m ∈ − 2 ,−1 ∪ ⟨0,+ ∞ ).

Łącząc wszystkie rozważone warunki otrzymujemy rozwiązanie

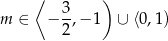
⟨ ) 3- m ∈ − 2,− 1 ∪ ⟨0 ,1)

 
Odpowiedź: ⟨ 3 ) m ∈ − 2,− 1 ∪ ⟨0,1)

Wersja PDF