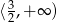/Szkoła średnia/Równania/Wymierne

Zadanie nr 2900648

Dodaj do ulubionych
Dodaj do rozwiązanych

Jednym z miejsc zerowych funkcji 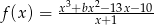x3+bx2−13x−10 f (x) = x+1 jest 5.

  • Znajdź współczynnik b .
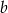  • Znajdź pozostałe miejsca zerowe funkcji f .
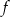  • Wyznacz przedziały monotoniczności funkcji.

Rozwiązanie

  • Wstawiamy 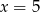x = 5 do wzoru funkcji i mamy równanie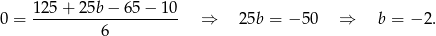
    12-5+--25b−--65−--10 0 = 6 ⇒ 25b = − 50 ⇒ b = − 2.

     
    Odpowiedź: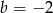 b = − 2

  • Musimy znaleźć pozostałe pierwiastki wielomianu
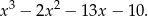
    x 3 − 2x 2 − 13x − 10.

    Wiemy, że 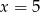x = 5 jest pierwiastkiem, dzielimy więc przez x − 5 .

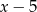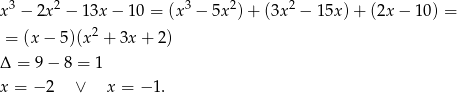
    x 3 − 2x 2 − 1 3x− 10 = (x3 − 5x 2)+ (3x 2 − 15x)+ (2x − 10) = 2 = (x − 5)(x + 3x+ 2) Δ = 9 − 8 = 1 x = − 2 ∨ x = − 1.

    Pierwiastek 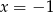x = − 1 odrzucamy, bo nie należy do dziedziny funkcji f .  
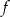    Odpowiedź: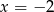 x = − 2

  • Na mocy poprzedniego podpunktu, funkcję 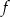f możemy zapisać w postaci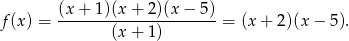
    f(x) = (x+--1)(x+--2)(x-−-5)-= (x+ 2)(x− 5). (x+ 1)

    Wykresem tej funkcji jest parabola bez jednego punktu (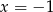x = − 1 nie należy do dziedziny!) o wierzchołku w punkcie 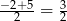−-2+5 3 2 = 2 . Zatem funkcja jest malejąca na zbiorze 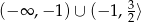(− ∞ ,− 1)∪ (− 1, 32⟩ i rosnąca na przedziale ⟨3,+ ∞ ) 2 .  
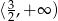    Odpowiedź: Malejąca na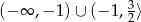 3 (− ∞ ,− 1)∪ (− 1,2 ⟩ , rosnąca na 3 ⟨2,+ ∞ )

Wersja PDF