/Szkoła średnia/Równania/Wymierne

Zadanie nr 3767428

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że żadna liczba całkowita nie jest rozwiązaniem równania 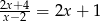2xx+−24= 2x + 1 .

Rozwiązanie

Oczywiście musi być 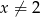x ⁄= 2 . Przy tym założeniu przekształcamy równanie.

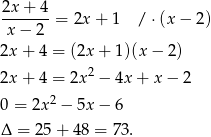
2x + 4 -------= 2x+ 1 / ⋅(x − 2) x − 2 2x+ 4 = (2x + 1)(x − 2 ) 2 2x+ 4 = 2x − 4x + x − 2 0 = 2x2 − 5x − 6 Δ = 25 + 4 8 = 73.

Ponieważ 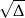√ -- Δ jest liczbą niewymierną, równanie to nie ma pierwiastków wymiernych.

Wersja PDF