/Szkoła średnia/Równania/Wymierne

Zadanie nr 5140564

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 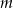m , dla których równanie 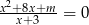x2+-8x+m-- x+3 = 0 ma dokładnie jedno rozwiązanie.

Rozwiązanie

Zauważmy, że ponieważ mamy 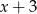x + 3 w mianowniku, 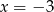x = − 3 nie należy do dziedziny równania. Mnożąc przez mianownik, mamy

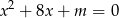
x2 + 8x + m = 0

Równanie to ma jeden pierwiastek jeżeli 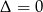Δ = 0 , czyli

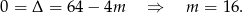
0 = Δ = 6 4− 4m ⇒ m = 16.

Pierwiastek ten wynosi 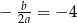b − 2a = − 4 .

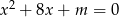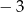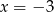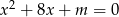Aby nie było zbyt łatwo, jest jeszcze jeden haczyk, mianowicie może zdarzyć się, że równanie x2 + 8x + m = 0 ma dwa rozwiązania, ale jedno z nich jest równe − 3 i wtedy wyjściowe równanie ma tylko jedno rozwiązanie! Sprawdźmy kiedy tak jest (podstawiamy x = − 3 do równania x 2 + 8x + m = 0 ).

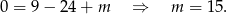
0 = 9− 24+ m ⇒ m = 15.

Ponieważ wiemy już, że dla 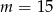m = 15 równanie 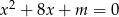2 x + 8x + m = 0 nie może mieć jednego pierwiastka, ma więc ono jeszcze jeden pierwiastek (różny od -3) i jest to jedyny pierwiastek wyjściowego równania.  
Odpowiedź: 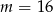m = 16 lub m = 15

Wersja PDF