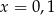/Szkoła średnia/Równania/Wymierne

Zadanie nr 7302921

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 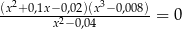(x2+-0,1x−0,02)(x3−0,008) x2−0,04 = 0 .

Rozwiązanie

Rozłóżmy najpierw wyrażenie w mianowniku

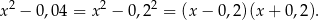
2 2 2 x − 0,04 = x − 0,2 = (x − 0,2)(x + 0,2).

Zatem dziedziną równania jest zbiór

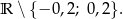
R ∖{ − 0,2; 0 ,2 }.

Rozkładamy teraz trójmian w pierwszym nawiasie w liczniku

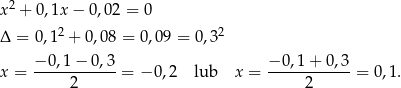
2 x + 0,1x − 0,02 = 0 Δ = 0,12 + 0,08 = 0,09 = 0,32 −-0,1-−-0,3- −-0,1-+-0,3- x = 2 = −0 ,2 lub x = 2 = 0,1.

Pierwsze z tych rozwiązań musimy odrzucić ze względu na dziedzinę równania.

Pozostało zająć się wyrażeniem w drugim nawiasie.

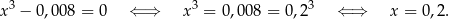
x3 − 0,008 = 0 ⇐ ⇒ x3 = 0,008 = 0,23 ⇐ ⇒ x = 0,2.

To rozwiązanie również nie należy do dziedziny równania.

Dane równanie ma więc tylko jedno rozwiązanie: 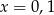x = 0 ,1 .  
Odpowiedź: x = 0,1

Wersja PDF