/Szkoła średnia/Równania/Wymierne

Zadanie nr 7389939

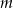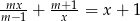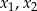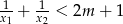Dla jakich wartości parametru m równanie -mx- m-+1 m −1 + x = x + 1 ma dwa różne pierwiastki x1,x 2 , spełniające warunek x1 + x1 < 2m + 1 1 2 .

Wersja PDF

Rozwiązanie

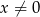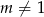Oczywiście musi być x ⁄= 0 i m ⁄= 1 . Przekształćmy dane równanie

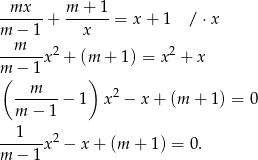
mx m + 1 ------ + ------ = x+ 1 / ⋅x m − 1 x --m---x 2 + (m + 1) = x 2 + x m( − 1 ) m 2 ------− 1 x − x+ (m + 1) = 0 m − 1 ---1--x 2 − x + (m + 1) = 0 . m − 1

Otrzymaliśmy więc zwykłe równanie kwadratowe z parametrem. Sprawdźmy, kiedy równanie to ma pierwiastki.

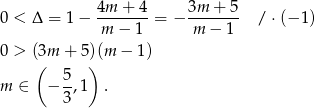
4m-+-4- 3m--+-5 0 < Δ = 1 − m − 1 = − m − 1 /⋅ (−1 ) 0 > ((3m + 5))(m − 1) 5- m ∈ − 3,1 .

Przy tym założeniu równanie ma dwa pierwiastki i możemy skorzystać ze wzorów Viète’a.

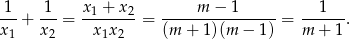
1 1 x 1 + x 2 m − 1 1 ---+ ---= -------- = ---------------- = ------. x1 x2 x1x2 (m + 1)(m − 1) m + 1

Rozwiązujemy nierówność.

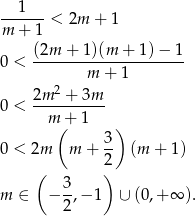
1 ------< 2m + 1 m + 1 (2m--+-1)(m-+--1)−--1 0 < m + 1 2 0 < 2m--+--3m- m + 1 ( 3) 0 < 2m m + -- (m + 1) ( 2) 3- m ∈ − 2 ,−1 ∪ (0,+ ∞ ).

W połączeniu z warunkiem na 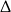Δ -ę otrzymujemy zatem

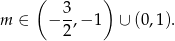
( ) 3 m ∈ − -,− 1 ∪ (0,1). 2

To jeszcze nie koniec, bo musimy sprawdzić, czy przypadkiem 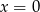x = 0 nie jest pierwiastkiem naszego równania. Sprawdzamy kiedy tak jest (podstawiamy 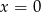x = 0 w równaniu kwadratowym).

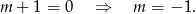
m + 1 = 0 ⇒ m = − 1.

Ta wartość 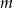m znajduje się poza naszym zbiorem rozwiązań, więc wszystko jest ok.  
Odpowiedź: m ∈ (− 3,− 1) ∪ (0,1) 2

Wersja PDF