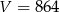/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny/Romb w podstawie

Zadanie nr 3781530

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa prostego jest romb. Krótsza przekątna rombu tworzy z krawędzią podstawy kąt 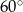60∘ i ma długość 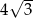√ -- 4 3 . Dłuższa przekątna graniastosłupa tworzy z dłuższą przekątną rombu kąt 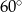6 0∘ . Oblicz objętość graniastosłupa.

Rozwiązanie

Zaczynamy od rysunku

PIC

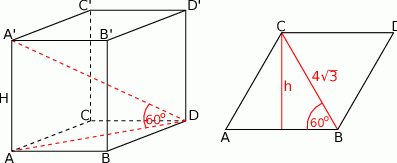
Wyznaczamy wysokość podstawy

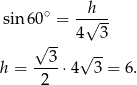
sin60 ∘ = -√h-- 4 3 √ 3- √ -- h = ----⋅4 3 = 6. 2

Zauważmy, że ponieważ 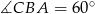∘ ∡CBA = 6 0 , więc trójkąt 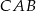CAB jest równoboczny. Zatem

√ -- |AB | = 4 3.

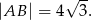
Policzmy pole rombu

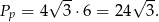
√ -- √ -- Pp = 4 3⋅ 6 = 24 3.

Z drugiej strony pole rombu możemy również policzyć z połowy iloczynu przekątnych. Stąd

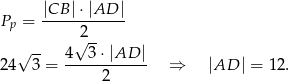
|CB |⋅|AD | Pp = ------------ √2-- 24√ 3 = 4--3-⋅|AD-|- ⇒ |AD | = 12. 2

Za pomocą funkcji trygonometrycznej wyznaczamy wysokość graniastosłupa

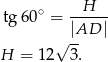
∘ --H--- tg60 = |AD | √ -- H = 12 3.

Teraz już łatwo policzyć objętość

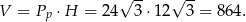
√ -- √ -- V = Pp ⋅H = 24 3 ⋅12 3 = 864.

 
Odpowiedź: V = 864

Wersja PDF