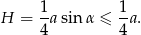/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny/Trójkąt w podstawie

Zadanie nr 3259848

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości a . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Uzasadnij, że wysokość graniastosłupa jest nie większa niż 1a 4 .

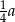Rozwiązanie

Oznaczmy przez 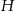H długość wysokości graniastosłupa, a przez α kąt przy wierzchołku trójkąta równoramiennego w podstawie.

PIC

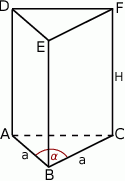
Pole podstawy jest równe

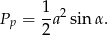
Pp = 1-a2sin α. 2

Z drugiej strony wiemy, że jest ono równe sumie pól dwóch ścian bocznych, czyli

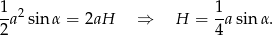
1-a2sin α = 2aH ⇒ H = 1a sin α. 2 4

Ponieważ 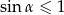sin α ≤ 1 , mamy stąd

1 1 H = -a sin α ≤ -a. 4 4
Wersja PDF