/Szkoła średnia/Zadania maturalne/Matura 2013
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 20 kwietnia 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 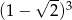 jest równa
jest równa
A) 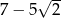 B)
B) 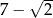 C)
C) 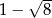 D)
D) 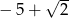
Liczba 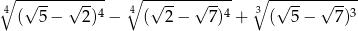 jest równa
jest równa
A) 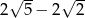 B)
B) 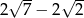 C)
C) 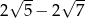 D)
D) 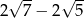
Liczba 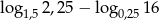 jest równa
jest równa
A) 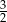 B) 4 C)
B) 4 C) 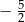 D) 0
D) 0
Marża równa 0,5% kwoty pożyczonego kapitału była równa 2 000 zł. Wynika stąd, że pożyczono
A) 4 000 zł B) 40 000 zł C) 200 000 zł D) 400 000 zł
Wskaż zbiór, w którym funkcja 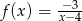 jest rosnąca.
jest rosnąca.
A) 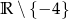 B)
B) 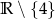 C)
C) 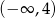 D)
D) 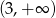
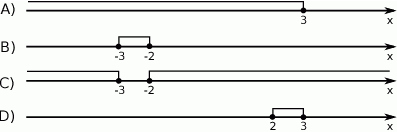
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 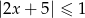 .
.
Miejscami zerowymi funkcji kwadratowej 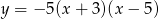 są
są
A) 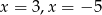 B)
B) 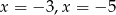 C)
C) 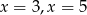 D)
D) 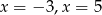
Jeden kąt trójkąta ma miarę 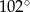 . Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
A) 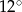 i
i 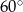 B)
B) 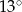 i
i 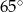 C)
C) 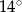 i
i 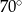 D)
D) 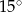 i
i 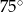
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 98. Zatem przeciwprostokątna ma długość:
A) 49 B) 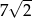 C) 7 D) 9
C) 7 D) 9
Wielomian 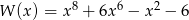 jest równy iloczynowi
jest równy iloczynowi
A) 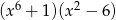 B)
B) 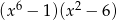 C)
C) 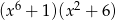 D)
D) 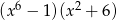
Pięciokąt 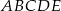 jest foremny. Wskaż trójkąt podobny do trójkąta
jest foremny. Wskaż trójkąt podobny do trójkąta 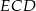
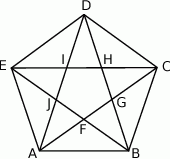
A)  B)
B) 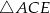 C)
C) 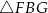 D)
D) 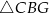
W prostokącie 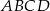 dane są
dane są 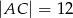 oraz
oraz 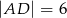 . Wówczas cosinus kąta
. Wówczas cosinus kąta 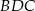 jest równy
jest równy
A) 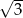 B)
B) 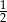 C)
C)  D)
D) 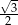
Równanie 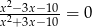
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie trzy rozwiązania
Suma 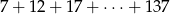 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 3888 B) 1944 C) 2016 D) 1800
Obwód kwadratu wpisanego w okrąg o długości 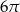 jest równy
jest równy
A) 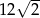 B)
B) 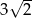 C)
C) 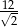 D)
D) 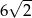
Ciąg 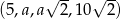 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 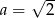 B)
B) 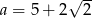 C)
C) 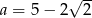 D)
D) 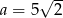
Kąt między cięciwą 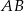 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 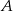 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 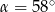 . Wówczas
. Wówczas
A)  B)
B) 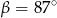 C)
C) 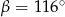 D)
D) 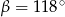
Na rysunku poniżej przedstawiony jest wykres funkcji liniowej  .
.
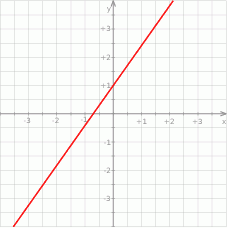
Funkcja ta może być określona wzorem
A) 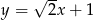 B)
B) 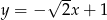 C)
C) 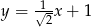 D)
D) 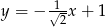
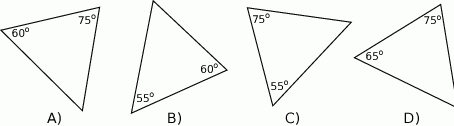
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 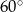 i
i 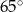 ?
?
Pole powierzchni jednej ściany sześcianu jest równe 9. Objętość tego sześcianu jest równa
A) 9 B) 27 C) 54 D) 81
Zdarzenia losowe  i
i 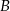 są rozłączne oraz
są rozłączne oraz 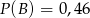 . Zatem prawdopodobieństwo zdarzenia
. Zatem prawdopodobieństwo zdarzenia 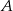 może być równe
może być równe
A) 0,63 B) 0,53 C) 0,73 D) 1
Objętość stożka wynosi 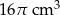 . Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 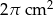 B)
B) 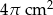 C)
C) 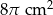 D)
D) 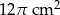
Okrąg o równaniu 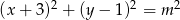 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 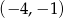 . Wtedy liczba
. Wtedy liczba 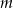 może być równa
może być równa
A) 25 B) 5 C) 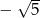 D)
D) 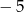
Zadania otwarte
Dane są funkcje 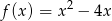 i
i 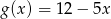 . Rozwiąż nierówność
. Rozwiąż nierówność 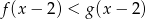 .
.
Rozwiąż równanie 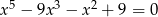 .
.
Uzasadnij, że jeśli liczby rzeczywiste 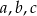 spełniają nierówności
spełniają nierówności 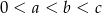 , to
, to
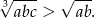
Ze zbioru liczb 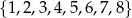 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 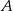 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 8.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 8.
W trójkącie równoramiennym 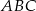 dane są
dane są 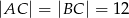 i
i 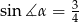 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 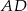 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 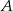 na bok
na bok 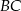 .
.
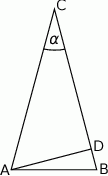
Uzasadnij, że jeżeli  jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 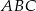 , w którym
, w którym  to
to 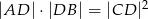 .
.
Ciąg geometryczny 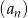 , gdzie
, gdzie  spełnia warunek
spełnia warunek 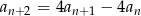 dla
dla 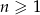 . Uzasadnij, że ciąg ten spełnia też warunek
. Uzasadnij, że ciąg ten spełnia też warunek 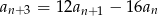 dla
dla 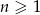 .
.
Ciąg 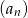 , gdzie
, gdzie 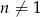 jest ciągiem arytmetycznym w którym
jest ciągiem arytmetycznym w którym 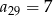 . Oblicz
. Oblicz 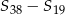 , gdzie
, gdzie 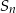 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 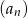 .
.
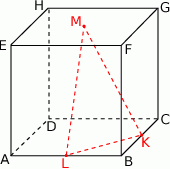
Punkty 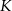 i
i 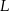 są środkami krawędzi
są środkami krawędzi 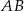 i
i 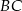 sześcianu
sześcianu 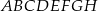 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 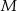 jest środkiem ściany
jest środkiem ściany 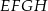 (zobacz rysunek). Oblicz pole trójkąta
(zobacz rysunek). Oblicz pole trójkąta  .
.
Napisz równanie okręgu, którego środek leży na prostej 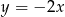 , i który przechodzi przez punkty
, i który przechodzi przez punkty 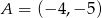 i
i 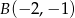 .
.

