/Szkoła średnia/Zadania maturalne/Matura 2013
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 6 kwietnia 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba osób planujących wziąć udział w demonstracji początkowo wzrosła o 20%, a po dwóch dniach zmalała o 30%. W wyniku tych dwóch zmian liczba osób planujących wziąć udział w demonstracji zmalała o
A) 16% B) 10% C) 56% D) 84%
Liczba 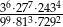 jest równa
jest równa
A) 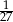 B) 243 C) 27 D)
B) 243 C) 27 D) 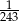
Liczba 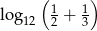 jest równa
jest równa
A) 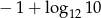 B) 10 C)
B) 10 C) 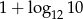 D)
D) 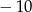
Równanie 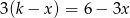 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 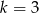 B)
B) 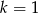 C)
C) 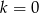 D)
D) 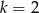
Wskaż liczbę, która spełnia równanie 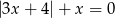 .
.
A) 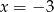 B)
B) 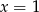 C)
C) 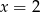 D)
D) 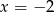
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
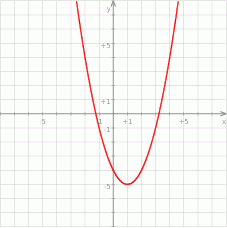
A) 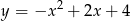 B)
B) 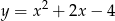 C)
C) 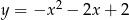 D)
D) 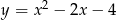
Pole działki budowlanej jest równe 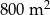 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 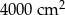 B)
B) 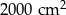 C)
C) 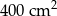 D)
D) 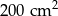
Przedział 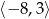 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 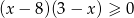
B) 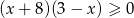
C) 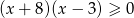
D) 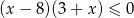
Jeśli 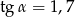 , to wartość wyrażenia
, to wartość wyrażenia 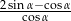 jest równa
jest równa
A) 0,8 B) 1,8 C) 2,6 D) 2,4
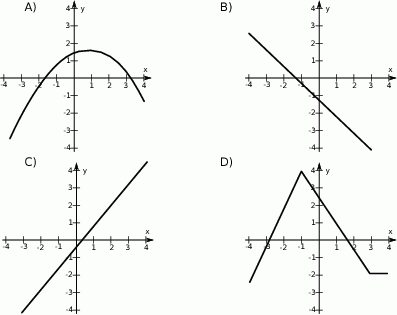
Wskaż wykres funkcji, która w przedziale 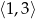 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
Równość 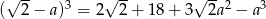 zachodzi dla
zachodzi dla
A) 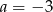 B)
B) 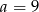 C)
C) 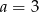 D)
D) 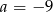
Punkt  jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
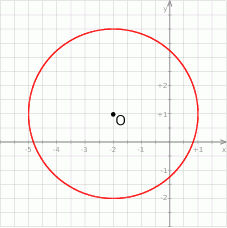
A) 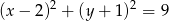
B) 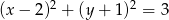
C) 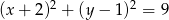
D) 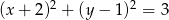
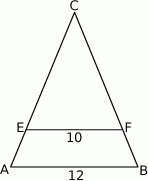
W trójkącie równoramiennym  dane są
dane są 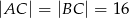 oraz
oraz 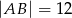 . Odcinek
. Odcinek 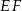 jest równoległy do podstawy
jest równoległy do podstawy 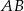 oraz
oraz 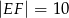 . Długość odcinka
. Długość odcinka 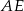 jest równa
jest równa
A) 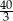 B)
B)  C)
C) 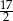 D)
D) 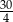
W trójkącie prostokątnym dwa dłuższe boki mają długości 7 i 9. Obwód tego trójkąta jest równy
A) 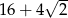 B)
B) 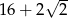 C)
C) 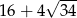 D)
D) 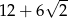
Ciąg 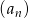 jest określony wzorem
jest określony wzorem 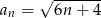 dla
dla 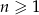 . Wówczas
. Wówczas
A) 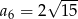 B)
B) 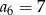 C)
C) 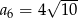 D)
D) 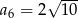
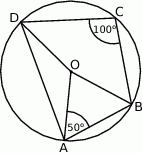
Punkt  jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
A) 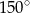 B)
B) 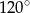 C)
C) 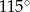 D)
D) 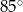
Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy 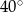 . Najmniejszy kąt tego czworokąta ma miarę
. Najmniejszy kąt tego czworokąta ma miarę
A) 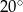 B)
B) 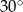 C)
C) 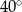 D)
D) 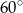
Pole rombu jest równe 54, a jedna z jego przekątnych jest 3 razy dłuższa od drugiej. Suma długości przekątnych jest równa
A) 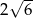 B) 24 C) 48 D)
B) 24 C) 48 D) 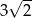
Promień okręgu wpisanego w trójkąt równoboczny jest o 3 krótszy od promienia okręgu opisanego na tym trójkącie. Wysokość trójkąta ma więc długość
A) 6 B) 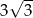 C)
C) 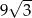 D) 9
D) 9
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 18 jest równa
A) 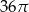 B)
B) 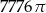 C)
C) 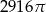 D)
D) 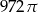
Prosta 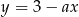 jest równoległa do prostej
jest równoległa do prostej 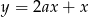 . Wtedy
. Wtedy
A) 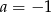 B)
B) 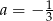 C)
C) 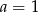 D)
D) 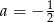
Przekątna sześcianu ma długość 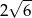 . Suma długości wszystkich krawędzi tego sześcianu wynosi
. Suma długości wszystkich krawędzi tego sześcianu wynosi
A) 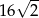 B)
B) 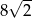 C)
C) 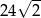 D) 48
D) 48
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 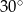 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 2 B) 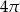 C)
C) 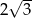 D)
D) 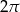
W trakcie zawodów sportowych ośmioro uczniów miało ustawić się w dwóch rzędach po 4 osoby. Na ile sposobów mogą ustawić się ci uczniowie?
A) 4 B) 576 C) 40320 D) 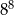
Na giełdzie kupiono tę samą liczbę akcji dwóch przedsiębiorstw, przy czym średnia cena zakupu jednej akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny akcji pierwszego przedsiębiorstwa. Ile średnio zapłacono za jedną akcję drugiego przedsiębiorstwa, jeżeli średnia cena zakupu wszystkich akcji wyniosła 90 zł?
A) 30 zł B) 60 zł C) 90 zł D) 120 zł
Zadania otwarte
Rozwiąż nierówność 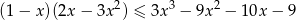 .
.
Iloczyn drugiego i czwartego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 9. Oblicz iloczyn pięciu początkowych kolejnych wyrazów tego ciągu.
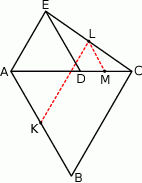
Trójkąty 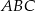 i
i 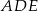 są równoboczne (zobacz rysunek). Punkty
są równoboczne (zobacz rysunek). Punkty 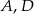 i
i 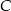 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 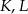 i
i 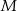 są środkami odcinków
są środkami odcinków 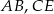 i
i 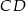 . Wykaż, że
. Wykaż, że 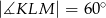 .
.
Podstawy trapezu prostokątnego mają długości 5 i 9 oraz cosinus kąta ostrego jest równy 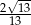 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Wyznacz równanie symetralnej odcinka o końcach 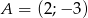 i
i 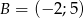 .
.
Wykaż, że jeżeli przy dzieleniu przez 5 jedna liczba daję resztę 2, a druga resztę 3, to iloczyn tych liczb daje przy dzieleniu przez 5 resztę 1.
Oblicz, ile jest liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie jedno 0, jest dokładnie jedna cyfra 6 i dokładnie jedna cyfra nieparzysta.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 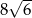 . Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 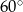 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 24 minut.

