/Szkoła średnia/Zadania maturalne/Matura 2013
Lubelska próba przed maturą
z matematyki (dla klas trzecich)
poziom podstawowy 24 stycznia 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 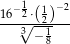 jest równa
jest równa
A) 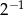 B)
B) 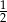 C)
C) 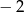 D) 1
D) 1
Wyrażenie 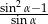 dla kąta ostrego
dla kąta ostrego  jest równe
jest równe
A) 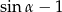 B)
B) 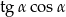 C)
C) 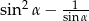 D)
D) 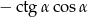
Liczbą odwrotną do liczby 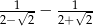 jest liczba
jest liczba
A) 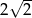 B)
B) 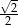 C)
C) 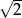 D) 2
D) 2
Jeżeli cena towaru brutto (23% podatku VAT) wynosi 1845 zł, to cena tego towaru netto jest równa
A) 1500 zł B) 1420,65 zł C) 424,35 zł D) 1424 zł
Liczba 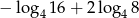 jest równa
jest równa
A) 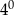 B)
B) 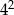 C)
C) 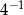 D)
D) 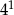
Wykresy funkcji liniowych 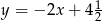 i
i 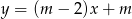 są prostymi prostopadłymi dla
są prostymi prostopadłymi dla
A) 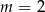 B)
B) 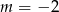 C)
C) 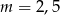 D)
D) 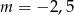
Wyrażenie 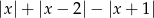 dla
dla 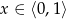 jest równe
jest równe
A) 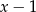 B)
B) 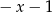 C)
C) 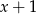 D)
D) 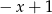
Funkcja określona wzorem 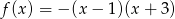 przyjmuje wartości ujemne dla
przyjmuje wartości ujemne dla
A) 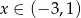
B) 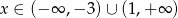
C) 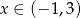
D) 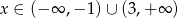
Jeśli jeden bok trójkąta ma długość 3 a drugi 5, to długość trzeciego boku nie może być równa
A) 9 B) 7 C) 6 D) 5
Jaka jest największa wartość funkcji kwadratowej 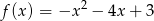 w przedziale
w przedziale 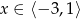 ?
?
A) 5 B) 7 C) 6 D) 8
Dla jakiego argumentu funkcja 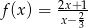 przyjmuje wartość 3?
przyjmuje wartość 3?
A) 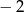 B) 2 C) 3 D) 0
B) 2 C) 3 D) 0
Prostokąt o bokach 4 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 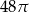 B)
B) 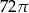 C)
C) 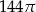 D)
D) 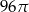
Punkty 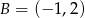 i
i 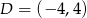 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 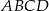 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 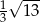 B)
B) 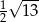 C)
C) 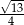 D)
D) 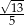
Pole wycinka koła (zacieniowana część na rysunku) jest równe
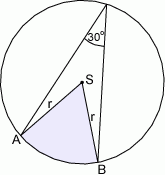
A) 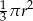 B)
B) 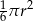 C)
C) 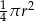 D)
D) 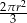
Stosunek pola kwadratu wpisanego w okrąg do pola kwadratu opisanego na tym okręgu wynosi
A) 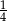 B)
B) 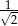 C)
C) 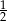 D)
D) 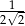
Kąt między ramionami trójkąta równoramiennego wynosi 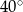 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 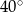 B)
B) 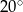 C)
C) 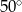 D)
D) 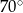
Suma dziesięciu początkowych wyrazów nieskończonego ciągu arytmetycznego 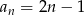 wynosi
wynosi
A) 80 B) 90 C) 110 D) 100
Odchylenie standardowe zestawu danych: 1, 3, 5, 7 jest równe
A) 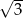 B) 3 C)
B) 3 C) 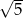 D) 5
D) 5
Jeżeli w ciągu geometrycznym 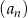 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 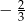 , a drugi wynosi 2, to
, a drugi wynosi 2, to
A) 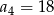 B)
B) 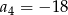 C)
C) 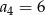 D)
D) 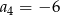
Liczbą, która nie należy do zbioru wartości funkcji 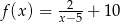 jest
jest
A) 0 B) 5 C) 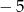 D) 10
D) 10
Funkcja
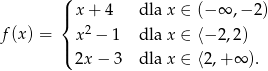
A) nie ma miejsc zerowych
B) ma trzy miejsca zerowe
C) ma jedno miejsce zerowe
D) ma dwa miejsca zerowe
Wskaż zbiór rozwiązań nierówności 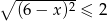 .
.
A) 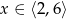 B)
B) 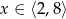 C)
C) 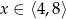 D)
D) 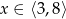
Dla pewnego zdarzenia losowego 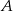 prawdziwe jest równanie (
prawdziwe jest równanie (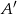 – zdarzenie przeciwne do zdarzenia
– zdarzenie przeciwne do zdarzenia 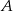 )
) 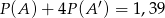 , zatem
, zatem
A) 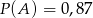 B)
B) 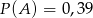 C)
C) 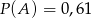 D)
D) 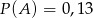
Zadania otwarte
Rozwiąż równanie 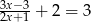 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 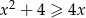 .
.
Dany jest ciąg 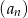 określony wzorem
określony wzorem 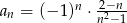 dla
dla 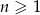 . Oblicz
. Oblicz 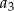 i
i 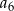 .
.
Dany jest prostokąt o bokach  i
i 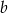 . Długość boku
. Długość boku  zmniejszono o 20% a długość boku
zmniejszono o 20% a długość boku 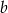 zwiększono o 10%. Oblicz, ile procent pola prostokąta o bokach
zwiększono o 10%. Oblicz, ile procent pola prostokąta o bokach  i
i 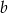 stanowi pole prostokąta otrzymanego po dokonaniu zmian długości boków.
stanowi pole prostokąta otrzymanego po dokonaniu zmian długości boków.
Oblicz dla jakich wartości parametrów 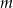 i
i  proste o równaniach:
proste o równaniach: 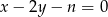 i
i 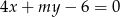 są dwiema różnymi prostymi równoległymi.
są dwiema różnymi prostymi równoległymi.
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 100, a pole powierzchni ścian bocznych 320. Oblicz objętość ostrosłupa.
Liczby 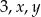 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zmniejszymy o 5, a liczbę
zmniejszymy o 5, a liczbę 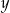 zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe
zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe  i
i 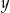 .
.
W trójkącie prostokątnym 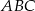 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 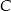 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 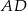 i
i 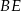 . Udowodnij, że
. Udowodnij, że 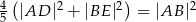 .
.
Punkty o współrzędnych 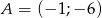 ,
, 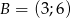 ,
, 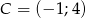 są wierzchołkami trapezu. Ramię trapezu
są wierzchołkami trapezu. Ramię trapezu 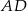 jest prostopadłe do podstaw
jest prostopadłe do podstaw 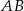 i
i 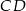 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 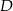 oraz pole powierzchni tego trapezu.
oraz pole powierzchni tego trapezu.

