/Szkoła średnia/Zadania maturalne/Matura 2013
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 27 kwietnia 2013 Czas pracy: 170 minut
Zadania zamknięte
Odwrotnością liczby 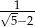 jest liczba:
jest liczba:
A) 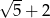 B)
B) 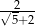 C)
C) 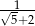 D)
D) 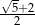
Pole kwadratu 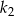 jest o 21% większe od pola kwadratu
jest o 21% większe od pola kwadratu 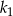 . Wówczas długość boku kwadratu
. Wówczas długość boku kwadratu 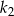 jest większa od długości boku kwadratu
jest większa od długości boku kwadratu 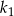 o
o
A) 10% B) 110% C) 21% D) 121%
Liczba ujemnych pierwiastków równania 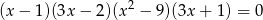 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Iloczyn 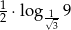 jest równy
jest równy
A) 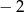 B)
B) 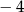 C)
C) 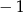 D) 1
D) 1
Liczba 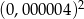 jest równa
jest równa
A) 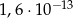 B)
B) 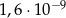 C)
C) 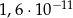 D)
D) 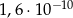
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 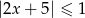 .
.
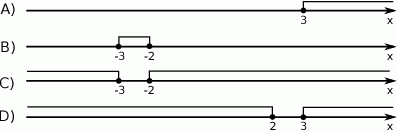
Wykresem funkcji kwadratowej 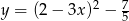 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 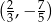 B)
B) 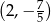 C)
C) 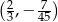 D)
D) 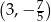
Funkcja liniowa 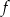 jest określona wzorem
jest określona wzorem 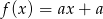 , gdzie
, gdzie 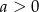 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 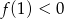 B)
B) 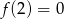 C)
C) 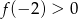 D)
D) 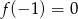
Różnica boków prostokąta jest równa 3, a przekątna tego prostokąta tworzy z jego bokiem kąt o mierze 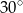 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 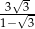 B)
B) 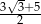 C)
C) 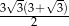 D)
D) 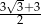
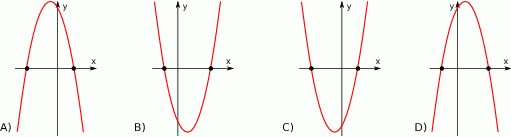
Dane są funkcje 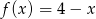 oraz
oraz  określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji  .
.
Kąt  jest ostry i
jest ostry i 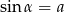 . Liczba
. Liczba  może być równa
może być równa
A) 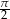 B)
B) 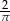 C)
C) 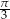 D)
D) 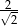
W trójkącie równoramiennym 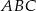 dane są
dane są 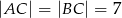 oraz wysokość
oraz wysokość 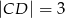 . Podstawa
. Podstawa 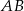 tego trójkąta ma długość
tego trójkąta ma długość
A) 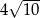 B)
B) 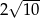 C)
C) 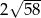 D) 10
D) 10
Wyrażenie 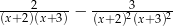 po sprowadzeniu do wspólnego mianownika ma postać
po sprowadzeniu do wspólnego mianownika ma postać
A) 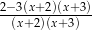 B)
B) 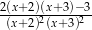 C)
C) 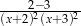 D)
D) 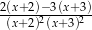
Ciąg 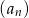 określony jest wzorem
określony jest wzorem 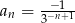 . Piąty wyraz tego ciągu to
. Piąty wyraz tego ciągu to
A) 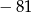 B)
B) 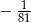 C) 81 D)
C) 81 D) 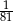
Zbiorem rozwiązań nierówności 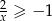 jest zbiór
jest zbiór
A) 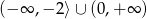 B)
B) 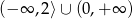 C)
C) 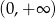 D)
D) 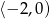
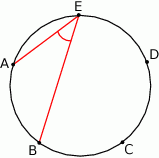
Punkty 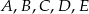 dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 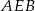 jest równa
jest równa
A) 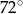 B)
B) 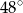 C)
C) 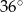 D)
D) 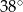
Każdą z sześciu krawędzi sześciokątnej ramki postanowiono pomalować na jeden z 10 kolorów, przy czym przeciwległe krawędzie mają mieć ten sam kolor, a żadne dwie sąsiednie krawędzie nie mogą mieć tego samego koloru. Liczba różnych możliwości pokolorowania ramki jest równa

A) 720 B) 1000 C) 30 D) 27
Wskaż 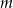 , dla którego proste
, dla którego proste 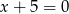 i
i 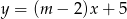 są prostopadłe.
są prostopadłe.
A) 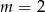 B)
B) 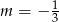 C)
C) 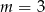 D)
D) 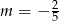
Punkt 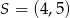 jest środkiem odcinka
jest środkiem odcinka 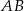 , w którym
, w którym 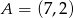 . Punkt
. Punkt 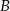 ma współrzędne:
ma współrzędne:
A) 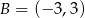 B)
B) 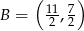 C)
C) 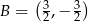 D)
D) 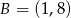
Pole powierzchni bocznej stożka jest dwa razy większe od jego pola podstawy. Tworząca tego stożka jest nachylona do płaszczyzny podstawy pod kątem
A) 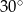 B)
B) 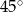 C)
C) 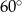 D)
D) 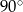
Punkty 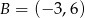 i
i 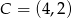 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 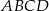 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 17 B) 113 C) 65 D) 29
Wiadomo, że mediana liczb 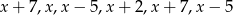 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
A) jest równa 3 B) jest równa 4 C) jest równa 5 D) może mieć dowolną wartość
Zadania otwarte
Rozwiąż nierówność 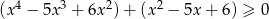 .
.
Rozwiąż równanie 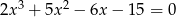 .
.
W sklepie budowlanym zakupiono 21 przedmiotów, przy czym średnia cena zakupu tych przedmiotów była równa 53 zł. Gdyby dodatkowo dokupiono miarkę, to średnia cena zakupionych przedmiotów zmalałaby do 51 zł. Jaka jest cena miarki?
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 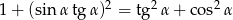 .
.
Jaką wysokość ma romb, jeżeli wiadomo, że jego przekątne mają długości 16 i 30?
Podaj przykład liczb naturalnych  i
i 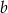 takich, że
takich, że 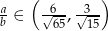 .
.
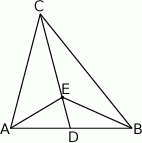
Na środkowej 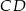 trójkąta
trójkąta 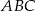 wybrano punkt
wybrano punkt 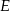 . Wykaż, że trójkąty
. Wykaż, że trójkąty 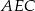 i
i 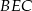 mają równe pola.
mają równe pola.
Ciąg 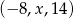 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 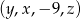 jest geometryczny. Oblicz
jest geometryczny. Oblicz 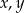 oraz
oraz  .
.
Dany jest trójkąt równoramienny 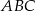 , w którym
, w którym 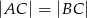 oraz
oraz 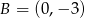 i
i 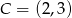 . Oś symetrii tego trójkąta ma równanie
. Oś symetrii tego trójkąta ma równanie 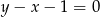 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 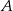 .
.
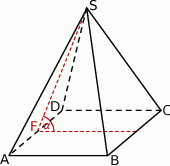
Dany jest ostrosłup prawidłowy czworokątny 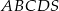 o podstawie
o podstawie 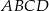 . Ramię trójkąta równoramiennego
. Ramię trójkąta równoramiennego 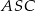 ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.