/Szkoła średnia/Zadania maturalne/Matura 2013
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 2 maja 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 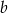 to 95% liczby
to 95% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 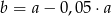 B)
B) 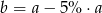 C)
C) 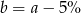 D)
D) 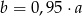
Liczba 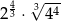 jest równa
jest równa
A) 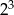 B)
B) 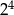 C)
C) 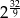 D)
D) 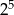
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 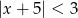 B)
B) 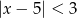 C)
C) 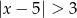 D)
D) 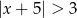
Jeżeli 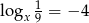 to liczba
to liczba  jest równa
jest równa
A) 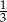 B) 3 C)
B) 3 C) 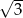 D)
D) 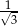
Funkcja liniowa 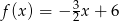 przyjmuje wartości ujemne dla:
przyjmuje wartości ujemne dla:
A) 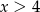 B)
B) 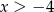 C)
C) 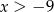 D)
D) 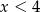
Liczbą odwrotną do 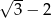 jest
jest
A) 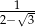 B)
B) 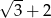 C)
C) 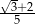 D)
D) 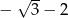
Rozwiązaniem równania 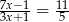 jest
jest
A) 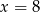 B)
B) 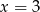 C)
C) 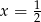 D)
D) 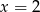
Dany jest ciąg 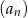 o wyrazie ogólnym
o wyrazie ogólnym 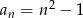 , gdzie
, gdzie 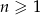 . Wówczas
. Wówczas
A) 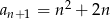 B)
B) 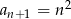 C)
C) 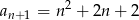 D)
D) 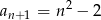
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 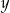 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 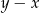 B)
B) 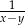 C)
C) 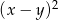 D)
D) 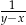
Iloczyn wielomianów 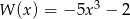 i
i 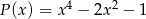 jest wielomianem stopnia
jest wielomianem stopnia
A) 7 B) 3 C) 5 D) 6
Rysunek przedstawia wykres funkcji 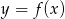 .
.
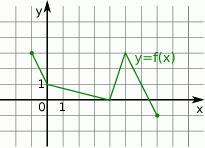
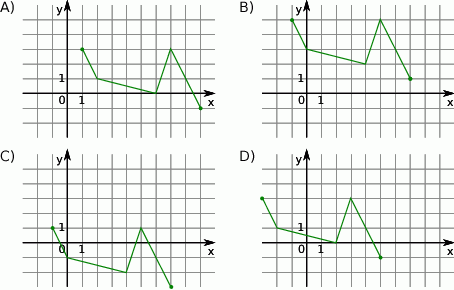
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 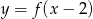 .
.
Suma 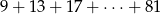 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 859 B) 851 C) 855 D) 1710
Zbiorem wartości funkcji 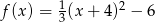 jest
jest
A) 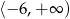 B)
B) 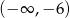 C)
C) 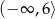 D)
D) 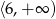
Zbiorem rozwiązań nierówności 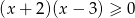 jest
jest
A) 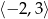
B) 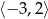
C) 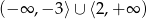
D) 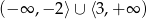
Który z podanych ciągów jest ciągiem geometrycznym?
A) 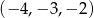 B)
B) 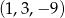 C)
C) 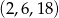 D)
D) 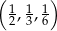
Kąt  jest ostry i
jest ostry i 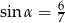 . Wówczas
. Wówczas 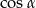 jest równy
jest równy
A) 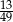 B)
B) 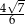 C)
C) 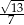 D)
D) 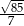
Wartość wyrażenia 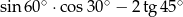 jest równa
jest równa
A) 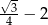 B)
B) 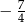 C)
C) 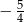 D)
D) 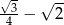
Wykres funkcji 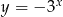 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) III i IV D) IV i I
Pole trójkąta prostokątnego równoramiennego wynosi 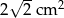 . Zatem przyprostokątna ma długość:
. Zatem przyprostokątna ma długość:
A) 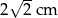 B)
B) 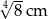 C)
C) 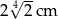 D)
D) 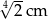
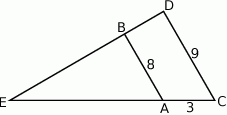
Oblicz długość odcinka 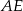 wiedząc, że
wiedząc, że 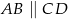 i
i 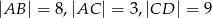 .
.
A) 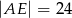 B)
B) 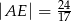 C)
C) 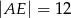 D)
D) 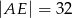
Punkty 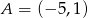 i
i 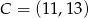 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 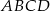 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 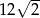 C) 20 D)
C) 20 D) 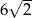
Punkty 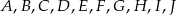 dzielą okrąg o środku
dzielą okrąg o środku 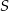 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 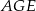 zaznaczonego na rysunku.
zaznaczonego na rysunku.
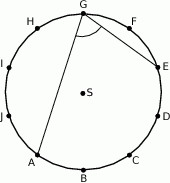
A) 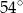 B)
B) 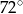 C)
C) 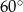 D)
D) 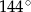
Pan Łukasz ma 3 marynarki, 8 par różnych spodni i 11 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 22 C) 132 D) 264
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 4.
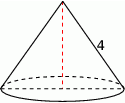
Pole powierzchni bocznej tego stożka jest równe
A) 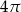 B)
B) 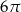 C)
C) 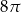 D)
D) 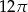
Prawdopodobieństwo zdarzenia 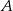 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 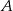 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 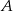 jest równe
jest równe
A) 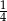 B)
B) 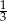 C)
C)  D)
D) 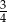
Zadania otwarte
Rozwiąż nierówność: 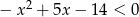 .
.
Wykaż, że jeżeli 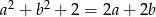 , to
, to 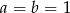 .
.
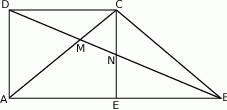
Punkt 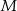 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 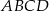 . Punkt
. Punkt 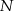 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 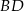 i wysokości
i wysokości 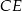 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 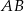 . Wykaż, że
. Wykaż, że 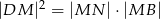 .
.
Wyznacz równania stycznych do okręgu 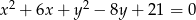 równoległych do osi
równoległych do osi 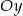 .
.
Iloraz ciągu geometrycznego 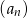 , gdzie
, gdzie 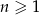 jest równy
jest równy 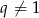 , a suma 10 początkowych wyrazów tego ciągu spełnia warunek
, a suma 10 początkowych wyrazów tego ciągu spełnia warunek 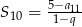 . Oblicz pierwszy wyraz tego ciągu.
. Oblicz pierwszy wyraz tego ciągu.
W trapezie prostokątnym krótsza przekątna ma długość ramienia trapezu i dzieli go na dwa trójkąty prostokątne. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Punkty 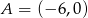 i
i 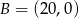 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 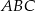 o przeciwprostokątnej
o przeciwprostokątnej 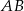 . Wierzchołek
. Wierzchołek 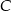 leży na prostej o równaniu
leży na prostej o równaniu 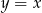 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 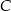 .
.
Dany jest graniastosłup prawidłowy trójkątny 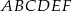 o podstawach
o podstawach 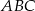 i
i 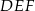 i krawędziach bocznych
i krawędziach bocznych 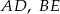 i
i 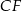 . Oblicz pole trójkąta
. Oblicz pole trójkąta 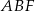 wiedząc, że
wiedząc, że 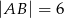 i
i 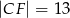 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 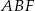 .
.
Kilku znajomych wybrało się na obiad, którego łączny koszt wyniósł 192 zł. Płacąc za obiad postanowili kwotę rachunku podzielić równo pomiędzy wszystkie obecne osoby. Okazało się jednak, że dwie osoby nie wzięły pieniędzy. W tej sytuacji każdy z pozostałych zapłacił o 8 zł więcej, niż powinien. Oblicz, ile osób uczestniczyło w obiedzie.

