/Szkoła średnia/Zadania maturalne/Matura 2013
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 4 czerwca 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 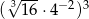 jest równa
jest równa
A) 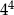 B)
B) 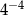 C)
C) 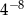 D)
D) 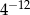
Dodatnia liczba  stanowi 70% liczby
stanowi 70% liczby 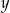 . Wówczas
. Wówczas
A) 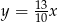 B)
B) 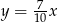 C)
C) 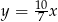 D)
D) 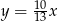
Przedział 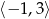 jest opisany nierównością
jest opisany nierównością
A) 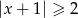 B)
B) 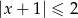 C)
C) 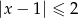 D)
D) 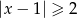
Wartość wyrażenia 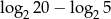 jest równa
jest równa
A) 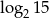 B) 2 C) 4 D)
B) 2 C) 4 D) 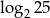
Liczba 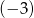 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 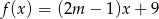 . Wtedy
. Wtedy
A) 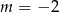 B)
B) 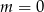 C)
C) 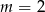 D)
D) 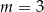
Dla każdego kąta ostrego  wyrażenie
wyrażenie 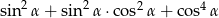 jest równe
jest równe
A) 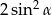 B)
B) 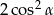 C) 1 D) 2
C) 1 D) 2
Kąt  jest ostry i
jest ostry i 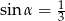 . Wartość wyrażenia
. Wartość wyrażenia 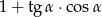 jest równa
jest równa
A) 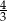 B)
B) 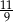 C)
C) 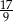 D)
D) 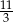
Zbiorem wartości funkcji 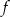 , której wykres przedstawiono na wykresie poniżej jest przedział
, której wykres przedstawiono na wykresie poniżej jest przedział
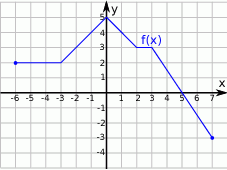
A) 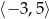 B)
B) 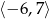 C)
C) 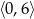 D)
D) 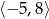
Na rysunku przedstawiony jest wykres funkcji 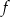 .
.
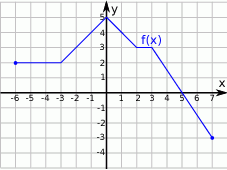
Przedziałem, w którym funkcja 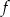 przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 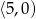 B)
B) 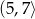 C)
C) 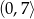 D)
D) 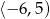
Na poniższych rysunkach przedstawiono wykresy funkcji 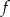 i
i 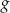 .
.
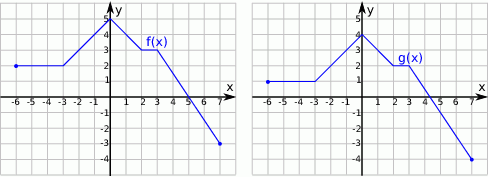
Funkcja 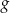 jest określona wzorem
jest określona wzorem
A) 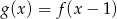 B)
B) 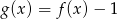 C)
C) 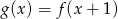 D)
D) 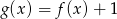
Punkt 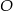 jest środkiem okręgu. Kąt
jest środkiem okręgu. Kąt  , zaznaczony na rysunku, ma miarę
, zaznaczony na rysunku, ma miarę
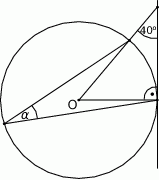
A) 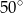 B)
B) 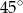 C)
C) 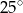 D)
D) 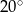
Iloczyn wielomianów 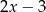 oraz
oraz 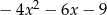 jest równy
jest równy
A) 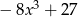 B)
B) 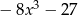 C)
C) 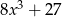 D)
D) 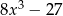
Prostokąt 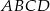 o przekątnej długości
o przekątnej długości 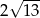 jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta
jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta 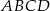 jest równy
jest równy
A) 10 B) 20 C) 5 D) 24
Cosinus kąta ostrego rombu jest równy 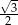 , bok rombu ma długość 3. Pole tego rombu jest równe
, bok rombu ma długość 3. Pole tego rombu jest równe
A)  B)
B) 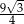 C)
C) 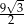 D) 6
D) 6
Pole powierzchni całkowitej sześcianu jest równe 12. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 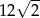 B)
B) 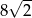 C)
C) 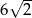 D)
D) 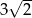
Ciąg 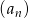 określony jest wzorem
określony jest wzorem 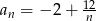 dla
dla 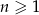 . Równość
. Równość 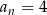 zachodzi dla
zachodzi dla
A) 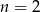 B)
B) 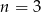 C)
C) 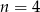 D)
D) 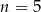
Funkcja 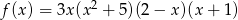 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie
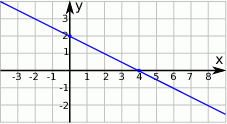
A) 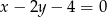 B)
B) 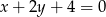 C)
C) 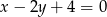 D)
D) 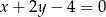
Przyprostokątne w trójkącie prostokątnym mają długości 1 i 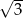 . Najmniejszy kąt w tym trójkącie ma miarę
. Najmniejszy kąt w tym trójkącie ma miarę
A) 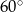 B)
B) 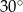 C)
C) 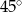 D)
D) 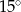
Dany jest ciąg arytmetyczny 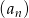 , w którym różnica
, w którym różnica 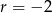 oraz
oraz 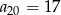 . Wówczas pierwszy wyraz tego ciągu jest równy
. Wówczas pierwszy wyraz tego ciągu jest równy
A) 45 B) 50 C) 55 D) 60
W ciągu geometrycznym 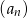 pierwszy wyraz jest równy
pierwszy wyraz jest równy 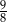 , a czwarty wyraz jest równy
, a czwarty wyraz jest równy 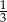 . Wówczas iloraz
. Wówczas iloraz 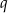 tego ciągu jest równy
tego ciągu jest równy
A) 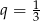 B)
B) 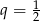 C)
C) 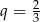 D)
D) 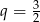
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
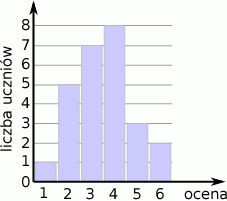
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
A) 2 B) 3 C) 3,5 D) 4
Objętość stożka o wysokości 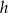 i promieniu podstawy trzy razy mniejszym od wysokości jest równa
i promieniu podstawy trzy razy mniejszym od wysokości jest równa
A) 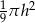 B)
B) 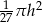 C)
C) 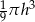 D)
D) 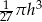
Rzucamy trzykrotnie symetryczną monetą. Prawdopodobieństwo, że w trzecim rzucie wypadnie orzeł jest równe
A) 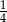 B)
B) 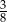 C)
C) 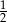 D)
D) 
Dana jest prosta 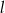 o równaniu
o równaniu 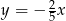 . Prosta
. Prosta 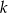 równoległa do prostej
równoległa do prostej 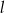 i przecinająca oś
i przecinająca oś 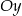 w punkcie o współrzędnych
w punkcie o współrzędnych 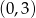 ma równanie
ma równanie
A) 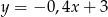 B)
B) 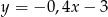 C)
C) 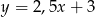 D)
D) 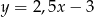
Liczba 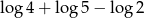 jest równa
jest równa
A) 10 B) 2 C) 1 D) 0
Zadania otwarte
Rozwiąż równanie 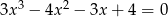 .
.
Kąt  jest ostry i
jest ostry i 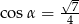 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 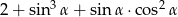 .
.
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których cyfra jedności jest o 3 większa od cyfry setek?
Wykaż, że liczba 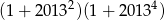 jest dzielnikiem liczby
jest dzielnikiem liczby
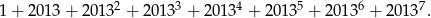
Nieskończony ciąg geometryczny 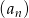 jest określony wzorem
jest określony wzorem 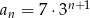 , dla
, dla 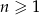 . Oblicz iloraz
. Oblicz iloraz 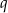 tego ciągu.
tego ciągu.
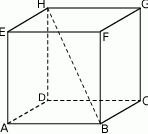
Podstawą graniastosłupa 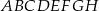 jest prostokąt
jest prostokąt 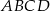 (zobacz rysunek), którego krótszy bok ma długość 3. Przekątna prostokąta
(zobacz rysunek), którego krótszy bok ma długość 3. Przekątna prostokąta 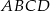 tworzy z jego dłuższym bokiem kąt
tworzy z jego dłuższym bokiem kąt 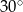 . Przekątna
. Przekątna 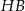 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 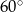 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
Grupa znajomych wykupiła wspólnie dostęp do Internetu na okres jednego roku. Opłata miesięczna wynosiła 120 złotych. Podzielono tę kwotę na równe części, by każdy ze znajomych płacił tyle samo. Po upływie miesiąca do grupy dołączyły jeszcze dwie osoby i wówczas opłata miesięczna przypadająca na każdego użytkownika zmniejszyła się o 5 złotych. Ile osób liczyła ta grupa w pierwszym miesiącu użytkowania Internetu?
Wierzchołki trapezu 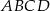 mają współrzędne:
mają współrzędne: 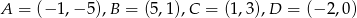 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 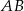 tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona
tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona 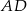 oraz
oraz 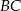 trapezu
trapezu 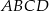 .
.

