/Szkoła średnia/Zadania maturalne/Matura 2013/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 23 marca 2013 Czas pracy: 170 minut
Zadania zamknięte
Ułamek 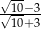 jest równy
jest równy
A) 1 B) 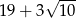 C)
C) 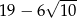 D)
D) 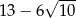
Jeśli długość jednego boku prostokąta zmniejszymy o 20%, a długość drugiego boku prostokąta zwiększymy o 5%, to pole prostokąta zmniejszy się o:
A) 12% B) 14% C) 15% D) 16%
Równanie 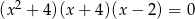 ma
ma
A) dwa rozwiązania: 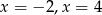
B) dwa rozwiązania: 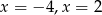
C) trzy rozwiązania: 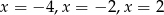
D) trzy rozwiązania: 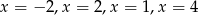
Iloczyn 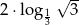 jest równy
jest równy
A) 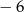 B)
B) 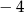 C)
C) 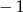 D) 1
D) 1
Liczbę  można przedstawić w postaci
można przedstawić w postaci
A) 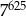 B)
B) 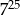 C)
C) 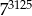 D)
D) 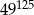
Zbiór rozwiązań nierówności 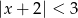 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności
A) 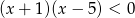
B) 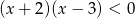
C) 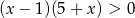
D) 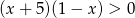
Dana jest parabola o równaniu 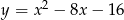 . Pierwsza współrzędna wierzchołka tej paraboli jest równa
. Pierwsza współrzędna wierzchołka tej paraboli jest równa
A) 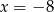 B)
B) 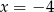 C)
C) 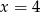 D)
D) 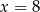
Zbiór wartości funkcji kwadratowej 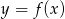 jest rozłączny z przedziałem
jest rozłączny z przedziałem 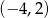 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 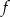 ?
?
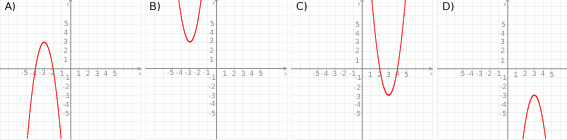
Dłuższy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 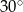 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 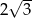 B)
B) 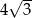 C)
C) 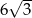 D) 12
D) 12
Funkcja liniowa 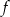 jest określona wzorem
jest określona wzorem 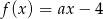 , gdzie
, gdzie 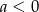 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 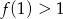 B)
B) 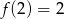 C)
C) 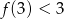 D)
D) 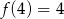
Kąt  jest ostry i
jest ostry i 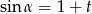 . Wtedy
. Wtedy
A) 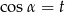 B)
B) 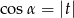 C)
C) 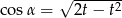 D)
D) 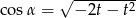
W trójkącie równoramiennym 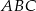 wysokość ma długość 8, a długość podstawy
wysokość ma długość 8, a długość podstawy 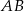 stanowi
stanowi 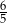 długości ramienia. Podstawa tego trójkąta ma długość
długości ramienia. Podstawa tego trójkąta ma długość
A) 30 B) 6 C) 12 D) 10
Wyrażenie 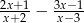 jest równe
jest równe
A) 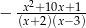 B)
B) 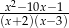 C)
C) 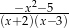 D)
D) 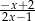
Ciąg 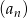 dany jest wzorem,
dany jest wzorem, 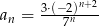 . Ciąg
. Ciąg 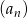 jest ciągiem
jest ciągiem
A) rosnącym B) malejącym C) geometrycznym D) arytmetycznym
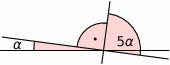
Miara kąta  jest równa:
jest równa:
A) 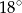 B)
B) 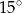 C)
C) 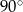 D)
D) 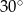
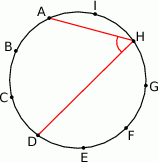
Punkty 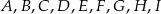 dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 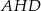 jest równa
jest równa
A) 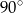 B)
B) 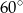 C)
C) 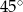 D)
D) 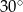
Na rysunku przedstawiony jest wykres funkcji 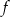 .
.
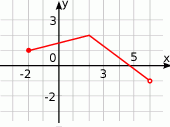
Wykres funkcji 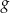 , określonej wzorem
, określonej wzorem 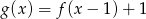 , przedstawia rysunek:
, przedstawia rysunek:
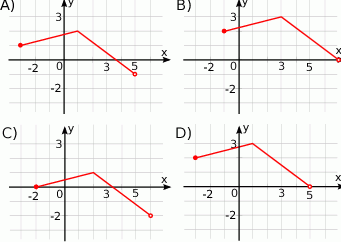
Prosta 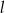 ma równanie
ma równanie 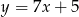 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 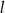 i przechodzącej przez punkt
i przechodzącej przez punkt 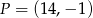 ma postać
ma postać
A) 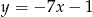 B)
B) 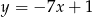 C)
C) 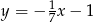 D)
D) 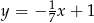
Jeżeli punkty 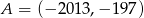 i
i 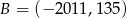 są końcami odcinka
są końcami odcinka 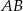 , to środkiem tego odcinka jest punkt o współrzędnych
, to środkiem tego odcinka jest punkt o współrzędnych
A) 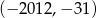 B)
B) 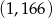 C)
C) 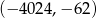 D)
D) 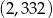
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 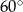 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 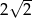 B)
B) 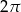 C)
C) 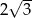 D) 2
D) 2
Punkty 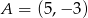 ,
, 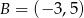 ,
, 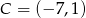 i
i 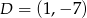 są wierzchołkami prostokąta
są wierzchołkami prostokąta 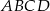 . Pole tego prostokąta jest równe
. Pole tego prostokąta jest równe
A) 16 B) 32 C) 64 D) 96
Pewna firma zatrudnia 7 osób. Dyrektor zarabia 7000 zł, a pensje pozostałych pracowników są równe: 4200 zł, 2800 zł, 2600 zł, 3400 zł, 3600 zł, 3000 zł. Mediana zarobków tych 7 osób jest równa
A) 3400 zł B) 3500 zł C) 3200 zł D) 7000 zł
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 11 kolorach, jest równa

A) 121 B) 110 C) 90 D) 21
Zadania otwarte
Rozwiąż nierówność 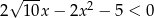 .
.
Rozwiąż równanie 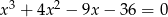 .
.
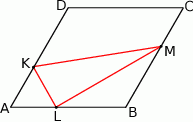
Na bokach 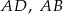 i
i 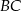 rombu
rombu 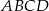 wybrano punkty
wybrano punkty 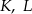 i
i 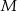 w ten sposób, że
w ten sposób, że 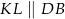 i
i 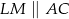 . Uzasadnij, że pole czworokąta
. Uzasadnij, że pole czworokąta 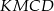 stanowi połowę pola rombu.
stanowi połowę pola rombu.
Wykaż, że jeżeli 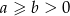 to
to
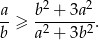
Średnia wieku w pewnej grupie uczniów jest równa 14 lat. Średnia wieku tych uczniów i ich opiekuna jest równa 16 lat. Opiekun ma 40 lat. Oblicz, ilu uczniów jest w tej grupie.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 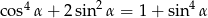 .
.
Dany jest romb, którego kąt ostry ma miarę 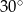 , a jego pole jest równe
, a jego pole jest równe 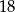 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Ciąg 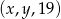 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 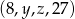 jest geometryczny. Oblicz
jest geometryczny. Oblicz 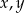 oraz
oraz  .
.
Zosia wrzucała do rzeki kamyki, przy czym w sumie wrzuciła 36 kamyków. Gdyby wrzucała kamyki ze średnią częstotliwością o 20% większą, to czas potrzebny na wrzucenie wszystkich kamyków skróciłby się o 12 sekund. Oblicz, ile średnio kamyków na sekundę wrzucała Zosia do rzeki.
Drewnianą kulę o promieniu 5 cm pocięto na 5 części w ten sposób, że płaszczyzny cięcia są prostopadłe do ustalonej średnicy 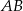 tej kuli, oraz podzieliły tę średnicę na 5 równych odcinków. Oblicz pola powierzchni otrzymanych przekrojów kołowych.
tej kuli, oraz podzieliły tę średnicę na 5 równych odcinków. Oblicz pola powierzchni otrzymanych przekrojów kołowych.