Zadanie nr 9033095
Uzasadnij, że żadna liczba rzeczywista nie jest rozwiązaniem równania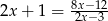 
.
Rozwiązanie
Sposób I
Przekształcamy dane równanie.
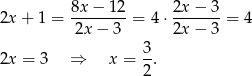
Otrzymane rozwiązanie nie jest jednak rozwiązaniem wyjściowego równania, bo dla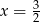 
zeruje się znajdujące się w mianowniku wyrażenie 
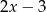(tzn. liczba 
nie należy do dziedziny równania). To oznacza, że wyjściowe równanie jest sprzeczne.
Sposób II
Przekształcamy dane równanie.
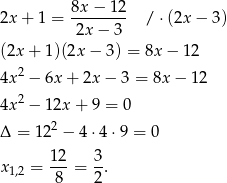
Otrzymane rozwiązanie nie jest jednak rozwiązaniem wyjściowego równania, bo dla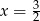 
zeruje się znajdujące się w mianowniku wyrażenie 
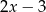(tzn. liczba 
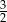nie należy do dziedziny równania). To oznacza, że wyjściowe równanie jest sprzeczne.
