/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Oblicz długość

Zadanie nr 1095850

Kąt ostry między przekątnymi równoległoboku 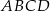ABCD ma miarę 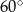∘ 60 . Przekątna 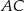AC ma długość 6, a przekątna 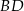BD jest prostopadła do boku 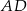AD . Oblicz długości boków równoległoboku.

Wersja PDF

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

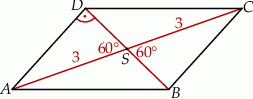
Ponieważ przekątne równoległoboku dzielą się na połowy, mamy 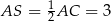AS = 12AC = 3 . Ponadto, ponieważ trójkąt 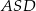ASD jest prostokątny, kąt 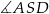∡ASD musi być ostry, czyli 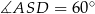∡ASD = 6 0∘ . Mamy zatem

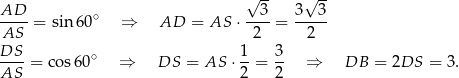
√ -- √ -- AD ∘ 3 3 3 ---- = sin 60 ⇒ AD = AS ⋅----= ----- AS 2 2 DS-- = cos 60∘ ⇒ DS = AS ⋅ 1-= 3- ⇒ DB = 2DS = 3. AS 2 2

Korzystamy teraz z twierdzenia Pitagorasa w trójkącie 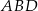ABD .

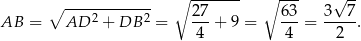
∘ ------- ∘ --- √ -- ∘ ------------ 27 63 3 7 AB = AD 2 + DB 2 = ---+ 9 = ---= ----. 4 4 2

 
Odpowiedź: 3√7- 3√-3- AB = 2 ,AD = 2

Wersja PDF