/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Oblicz długość

Zadanie nr 1618458

Długości boków równoległoboku 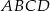ABCD wynoszą 1 i 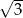√ -- 3 , a kąt przy wierzchołku 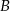B ma miarę 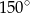150∘ . Oblicz promień okręgu opisanego na trójkącie ABD .

Wersja PDF

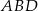Rozwiązanie

Zaczynamy od rysunku. Oczywiście 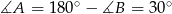∘ ∘ ∡A = 180 − ∡B = 30 .

PIC

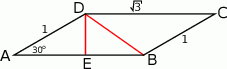
Plan jest następujący: wyliczymy długość przekątnej 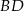BD , a potem z twierdzenia sinusów wyliczymy promień okręgu opisanego na trójkącie ABD .

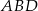Sposób I

Długość przekątnej 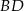BD możemy łatwo wyliczyć z twierdzenia cosinusów w trójkącie ABD .

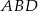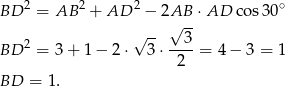
BD 2 = AB 2 + AD 2 − 2AB ⋅ AD cos30 ∘ √ -- √ -- BD 2 = 3+ 1− 2⋅ 3⋅ --3-= 4 − 3 = 1 2 BD = 1.

Zatem szukany promień jest równy

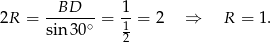
-BD---- 1- 2R = sin 30∘ = 1 = 2 ⇒ R = 1. 2

Zamiast korzystać z twierdzenia sinusów, mogliśmy też skorzystać zez wzoru na pole 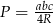P = a4bRc . Użycie twierdzenia sinusów jest jednak szybsze.

Sposób II

Jeżeli dorysujemy wysokość 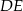DE w trójkącie 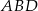ABD to mamy

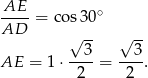
AE ∘ AD-- = cos 30 √ -- √ -- AE = 1 ⋅--3-= --3-. 2 2

Zatem 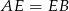AE = EB , co oznacza, że trójkąt 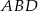ABD jest równoramienny (wysokość jest symetralną boku). Zatem 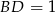BD = 1 . Promień liczymy jak poprzednio.  
Odpowiedź: 1

Wersja PDF