Zadanie nr 5639110
Wysokości równoległoboku mają długości 2 i 4. Oblicz pole równoległoboku wiedząc, że jego obwód wynosi 30.
Rozwiązanie
Narysujmy szkicowy rysunek i oznaczmy boki równoległoboku przez  i
i 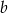 .
.
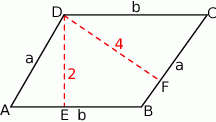
Mamy wtedy
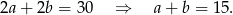
Drugie równanie dostaniemy pisząc dwa wzory na pole równoległoboku
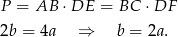
Podstawiając to do wcześniejszego równania, mamy
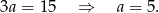
Zatem pole wynosi
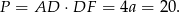
Odpowiedź: 20

