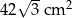/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Pole

Zadanie nr 6350645

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole równoległoboku o bokach 7 cm i 12 cm, w którym dwa sąsiednie kąty różnią się o 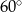60 ∘ .

Rozwiązanie

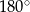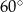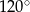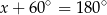Ponieważ suma dwóch sąsiednich kątów równoległoboku jest równa ∘ 18 0 , z podanej informacji wynika, że kąty równoległoboku to 60∘ i 12 0∘ (jak ktoś nie wie jak to wymyślić, to niech rozwiąże równanie x + 60∘ = 1 80∘ ).

PIC

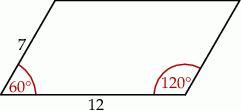
Korzystamy teraz z wzoru na pole równoległoboku

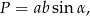
P = ab sinα ,

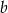gdzie α jest kątem między bokami długości a i b . W naszej sytuacji mamy

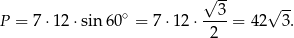
√ -- ∘ --3- √ -- P = 7 ⋅12 ⋅sin60 = 7⋅ 12⋅ 2 = 42 3.

 
Odpowiedź: 42√ 3-cm 2

Wersja PDF