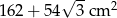/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Pole

Zadanie nr 7776354

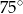Przekątna równoległoboku, poprowadzona z wierzchołka kąta rozwartego, ma długość 18 cm i dzieli ten kąta na kąty o miarach 4 5∘ i 75∘ . Oblicz pole równoległoboku. Wynik przedstaw w postaci 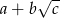√ - a+ b c , gdzie 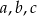a ,b ,c są liczbami naturalnymi.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

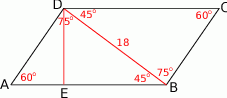
Znając kąty na jakie dzieli kąt rozwarty przekątna 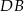DB łatwo wyliczyć miarę kąta ostrego równoległoboku (patrzymy na trójkąt DAB )

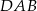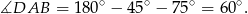
∡DAB = 180 ∘ − 4 5∘ − 75∘ = 60∘.

Dorysujmy teraz wysokość 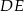DE . Z trójkąta prostokątnego 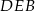DEB łatwo wyliczyć długości odcinków 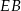EB i DE .

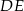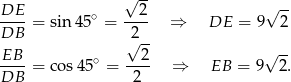
√ -- DE ∘ 2 √ -- ----= sin45 = ---- ⇒ DE = 9 2 DB √2-- EB--= cos 45∘ = --2- ⇒ EB = 9√ 2. DB 2

Podobnie, z trójkąta 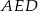AED wyliczamy długość odcinka AE .

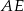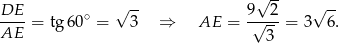
√ -- DE-- ∘ √ -- 9--2- √ -- AE = tg 60 = 3 ⇒ AE = √ 3 = 3 6.

W takim razie

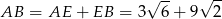
√ -- √ -- AB = AE + EB = 3 6+ 9 2

i pole jest równe

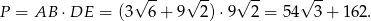
√ -- √ -- √ -- √ -- P = AB ⋅DE = (3 6+ 9 2) ⋅9 2 = 54 3+ 1 62.

 
Odpowiedź: √ -- 162 + 54 3 cm 2

Wersja PDF