Zadanie nr 1823597
Niech  i
i 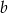 będą długościami kolejnych boków równoległoboku
będą długościami kolejnych boków równoległoboku 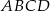 , zaś
, zaś 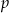 i
i  długościami jego przekątnych. Wykaż, że
długościami jego przekątnych. Wykaż, że 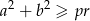 .
.
Rozwiązanie
Szkicujemy równoległobok.
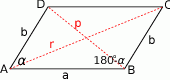
Sposób I
Jak wiadomo w każdym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości jego boków, tzn.
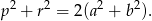
Musimy zatem wykazać nierówność
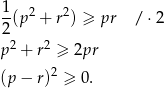
Nierówność ta jest oczywiście spełniona.
Sposób II
Jeżeli nie chcemy korzystać z twierdzenia o przekątnych równoległoboku, to możemy sami je udowodnić.
Stosując twierdzenia cosinusów w trójkątach 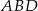 i
i 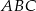 mamy
mamy
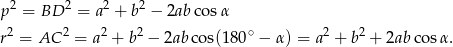
Dodając te nierówności stronami mamy
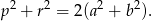
Nierówność uzasadniamy tak jak w I sposobie.

