Zadanie nr 3052246
Wykaż, że proste przechodzące przez wierzchołek równoległoboku i środki boków, do których on nie należy, dzielą przekątną równoległoboku na trzy równe części.
Rozwiązanie
Niech 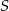 będzie środkiem równoległoboku,
będzie środkiem równoległoboku, 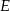 i
i 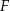 niech będą środkami odpowiednio boków
niech będą środkami odpowiednio boków 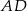 i
i 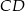 , a
, a 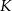 i
i 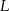 niech będą punktami przecięcia odcinków
niech będą punktami przecięcia odcinków 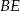 i
i 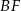 z przekątną
z przekątną 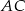 . W szczególności punkt
. W szczególności punkt 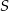 jest środkiem odcinków
jest środkiem odcinków 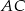 i
i 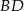 (bo przekątne równoległoboku dzielą się na połowy).
(bo przekątne równoległoboku dzielą się na połowy).
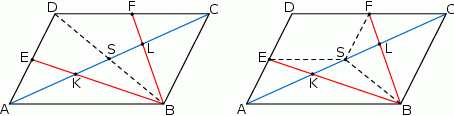
Musimy wykazać, że 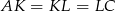 .
.
Sposób I
Dorysujmy przekątną 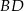 trapezu. Odcinki
trapezu. Odcinki 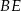 i
i 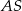 są środkowymi w trójkącie
są środkowymi w trójkącie 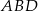 , więc dzielą się w stosunku 2:1 (licząc od wierzchołka). W szczególności
, więc dzielą się w stosunku 2:1 (licząc od wierzchołka). W szczególności
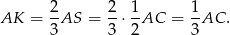
Podobnie, w trójkącie 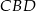 środkowe
środkowe 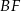 i
i 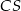 dzielą się w stosunku 2:1, więc
dzielą się w stosunku 2:1, więc
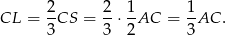
To oznacza, że
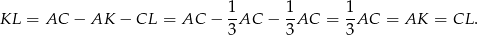
Sposób II
Tym razem dorysujmy odcinki 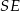 i
i 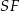 . Czworokąt
. Czworokąt 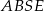 jest trapezem, więc trójkąty
jest trapezem, więc trójkąty 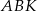 i
i 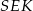 są podobne (bo mają równe kąty) w skali
są podobne (bo mają równe kąty) w skali
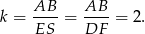
W takim razie
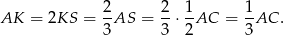
Analogicznie, patrząc na trapez 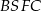 i podobieństwo trójkątów
i podobieństwo trójkątów 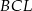 i
i 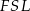 uzasadniamy, że
uzasadniamy, że
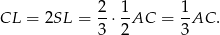
Równość 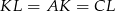 uzasadniamy tak samo jak w pierwszym sposobie.
uzasadniamy tak samo jak w pierwszym sposobie.
Sposób III
Tym razem dorysujmy odcinki 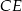 i
i 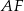 .
.
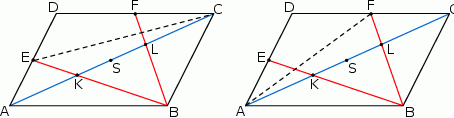
Czworokąt 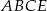 jest trapezem, więc trójkąty
jest trapezem, więc trójkąty 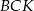 i
i 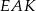 są podobne (bo mają równe kąty) w skali
są podobne (bo mają równe kąty) w skali
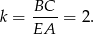
To oznacza, że
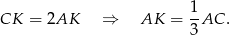
Analogicznie, patrząc na trapez 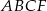 i podobieństwo trójkątów
i podobieństwo trójkątów 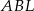 i
i 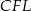 mamy
mamy
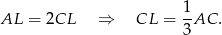
Równość 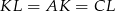 uzasadniamy tak samo jak w pierwszym sposobie.
uzasadniamy tak samo jak w pierwszym sposobie.

