Zadanie nr 3097507
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.
Rozwiązanie
Zaczynamy od rysunku.
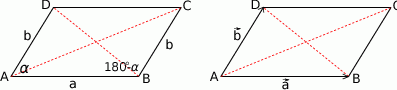
Sposób I
Jeżeli przyjmiemy oznaczenia jak na rysunku to z twierdzenia cosinusów w trójkącie 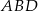 mamy
mamy
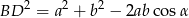
Z twierdzenia cosinusów w trójkącie 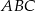 mamy
mamy
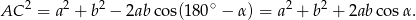
Dodając te dwie równości stronami mamy
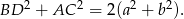
Sposób II
Tym razem użyjemy rachunku wektorowego i podstawowych własności iloczynu skalarnego. Jeżeli oznaczymy 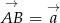 i
i 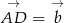 to mamy
to mamy
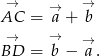
Zatem
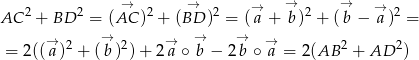
Sposób III
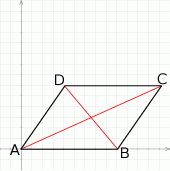
Tym razem narysujmy sobie równoległobok w układzie współrzędnych. Możemy tak wybrać układ współrzędnych, że 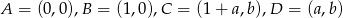 .
.
Kwadraty długości ramion są więc równe
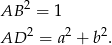
Policzmy teraz sumę kwadratów długości przekątnych.
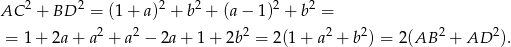
Sposób IV
Tym razem zrzutujmy wierzchołki 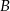 i
i 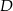 (czyli wierzchołki przy większych kątach równoległoboku) na przekątną
(czyli wierzchołki przy większych kątach równoległoboku) na przekątną 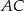 .
.
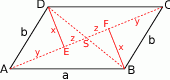
Przyjmując oznaczenia z obrazka mamy
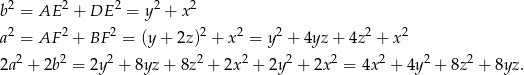
Z drugiej strony