Zadanie nr 3363321
Dany jest równoległobok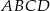 
. Okrąg wpisany w trójkąt 
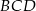jest styczny do przekątnej 
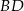w punkcie 
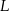, a okrąg wpisany w trójkąt 
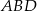ma środek 
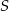i jest styczny do boku 
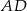w punkcie 
.
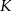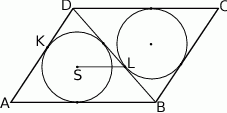
Wykaż, że jeżeli odcinek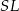 
jest równoległy do prostej 
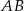, to 
.
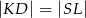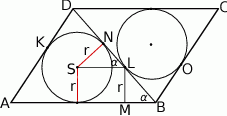
Rozwiązanie
Niech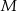 
będzie rzutem punktu 
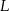na bok 
, 
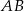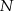niech będzie rzutem 
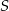na przekątn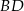ą 
, a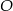 
niech będzie punktem styczności okręgu wpisanego w trójkąt 
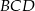z bokiem 
.
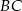Trójkąty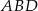 
i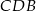 
są przystające, więc odpowiadające sobie odcink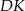i 
i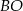 
łączące wierzchołk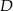i 
i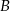 
tych trójkątów z punktami stycznośc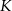i 
i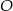 
okręgów wpisanych w te trójkąty są równe. Zatem
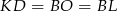
(skorzystaliśmy z tego, że odcinki stycznych do okręgu poprowadzonych z punktu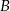 
mają tę samą długość). Wystarczy zatem udowodnić, że 
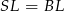. Aby to zrobić patrzymy na trójkąty prostokątne 
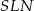i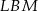 
. Trójkąty te mają wspólny kąt
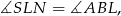
bo proste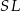 
i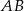 
są równoległe. Ponadto
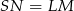
To oznacza, że trójkąty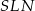 
i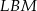 
są przystające i ich przeciwprostokątne mają równe długości
