Zadanie nr 7211547
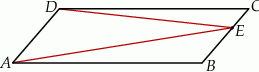
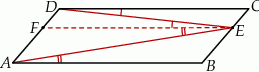
Na rysunku przedstawiono równoległobok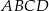 
i trójkąt 
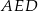. Punkt 
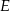leży na odcinku 
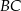. Uzasadnij, że pole równoległoboku 
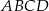jest dwa razy większe od pola trójkąta 
.
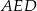Rozwiązanie
Sposób I
Dorysujmy odcinek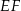 
równoległy do podstawy 
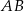równoległoboku.
Zauważmy teraz, że trójkąty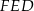 
i 
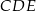są przystające. Przystające są też trójkąty 
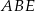i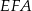 
. W takim razie
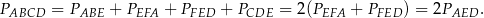
Sposób II
Zauważmy, że wysokość trójkąta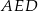 
opuszczona z wierzchołka 
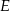jest jednocześnie wysokością równoległoboku opuszczoną na bok 
.
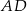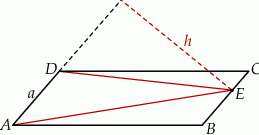
Mamy zatem
