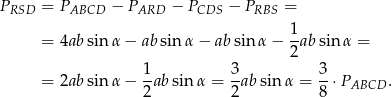Zadanie nr 8524178
Punkty 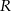 i
i 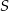 są środkami boków odpowiednio
są środkami boków odpowiednio 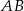 i
i 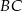 równoległoboku
równoległoboku 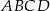 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 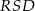 jest równe
jest równe pola tego równoległoboku.
pola tego równoległoboku.
Rozwiązanie
Oznaczmy 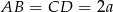 ,
, 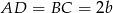 i
i 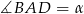 .
.
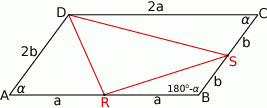
Mamy zatem
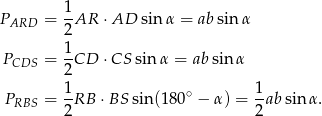
Stąd
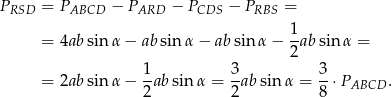
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 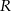 i
i 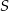 są środkami boków odpowiednio
są środkami boków odpowiednio 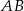 i
i 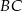 równoległoboku
równoległoboku 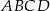 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 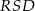 jest równe
jest równe pola tego równoległoboku.
pola tego równoległoboku.
Oznaczmy 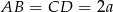 ,
, 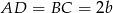 i
i 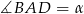 .
.

Mamy zatem
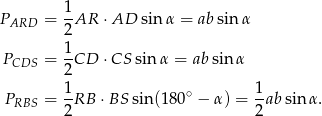
Stąd