/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Udowodnij

Zadanie nr 9165340

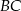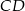Na bokach BC i CD równoległoboku 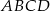ABCD zbudowano kwadraty 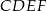CDEF i BCGH (zobacz rysunek).

PIC

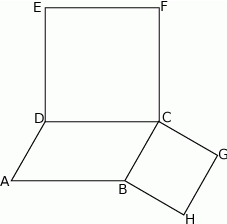
Udowodnij, że 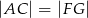|AC | = |FG | .

Wersja PDF

Rozwiązanie

Sposób I

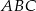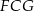Wystarczy pokazać, że trójkąty ABC i FCG są przystające (bo wtedy AC = FG ).

PIC

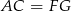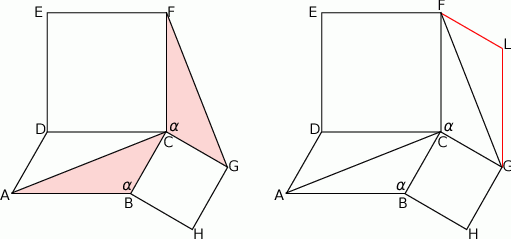
Mają one dwie pary równych boków

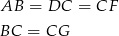
AB = DC = CF BC = CG

oraz jeżeli oznaczymy 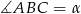∡ABC = α to

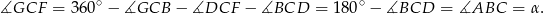
∘ ∘ ∡GCF = 3 60 − ∡GCB − ∡DCF − ∡BCD = 18 0 − ∡BCD = ∡ABC = α .

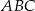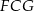Zatem rzeczywiście trójkąty ABC i FCG są przystające.

Sposób II

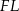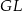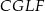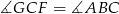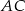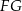Tym razem dorysujmy odcinki FL i GL tak, aby otrzymać równoległobok CGLF . Podobnie jak poprzednio uzasadniamy, że ∡GCF = ∡ABC . Równoległoboki te mają też równe boki, więc są przystające. W takim razie ich dłuższe przekątne AC i FG mają równe długości.

Wersja PDF