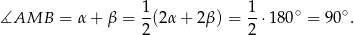Zadanie nr 9300558
W równoległoboku 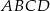 , w którym
, w którym 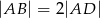 punkt
punkt 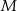 jest środkiem boku
jest środkiem boku 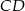 . Wykaż, że trójkąt
. Wykaż, że trójkąt 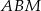 jest prostokątny.
jest prostokątny.
Rozwiązanie
rozpoczynamy od rysunku.
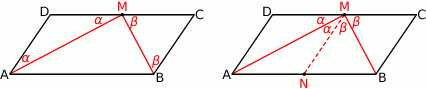
Zauważmy, że ponieważ 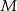 jest środkiem boku
jest środkiem boku 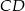 i
i 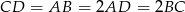 , trójkąty
, trójkąty 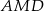 i
i 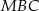 są równoramienne. Oznaczmy
są równoramienne. Oznaczmy 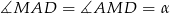 i
i 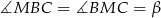 .
.
Sposób I
Zauważmy, że 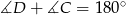 . Zależność ta pozwoli uzyskać zależność między kątami
. Zależność ta pozwoli uzyskać zależność między kątami  i
i 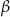 . Liczymy
. Liczymy
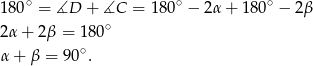
Zatem
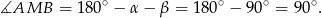
Sposób II
Niech 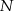 będzie środkiem boku
będzie środkiem boku 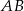 . Czworokąt
. Czworokąt 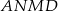 jest równoległobokiem oraz
jest równoległobokiem oraz 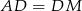 . Jest to więc romb. Analogicznie zauważamy, że czworokąt
. Jest to więc romb. Analogicznie zauważamy, że czworokąt 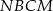 jest rombem. Ponieważ przekątne w rombie są dwusiecznymi jego kątów wewnętrznych, mamy
jest rombem. Ponieważ przekątne w rombie są dwusiecznymi jego kątów wewnętrznych, mamy 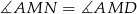 i
i 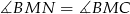 . W takim razie
. W takim razie