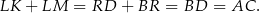Zadanie nr 4689584
Na bokach 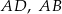 i
i 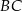 kwadratu
kwadratu 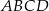 wybrano punkty
wybrano punkty 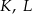 i
i 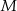 w ten sposób, że
w ten sposób, że 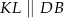 i
i 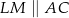 . Uzasadnij, że
. Uzasadnij, że 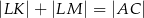 .
.
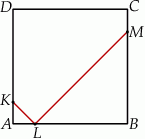
Rozwiązanie
Sposób I
Oznaczmy 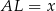 i
i 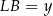 . Trójkąty
. Trójkąty 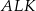 i
i 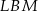 są prostokątne i mają kąty ostre równe
są prostokątne i mają kąty ostre równe 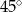 , więc są to trójkąty równoramienne.
, więc są to trójkąty równoramienne.
Zatem 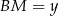 i mamy
i mamy
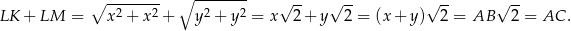
Sposób II
Poprowadźmy przez punkty 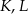 i
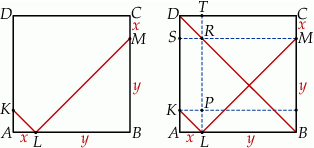
i 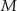 proste równoległe do boków kwadratu (prawy rysunek). Otrzymane czworokąty
proste równoległe do boków kwadratu (prawy rysunek). Otrzymane czworokąty 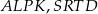 i
i 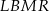 są kwadratami, w dodatku kwadraty
są kwadratami, w dodatku kwadraty 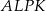 i
i 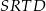 są przystające. Zatem
są przystające. Zatem