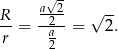/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat/Udowodnij

Zadanie nr 5793653

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że stosunek długości promienia okręgu opisanego na kwadracie do długości promienia wpisanego w ten kwadrat jest równy 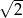√ -- 2 .

Rozwiązanie

Oznaczmy przez a długość boku kwadratu.

PIC

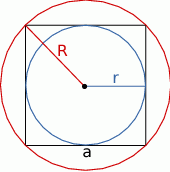
Promień okręgu opisanego na kwadracie to połowa przekątnej kwadratu, więc promień ten jest równy 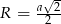√ - R = a-2- 2 . Promień okręgu wpisanego to połowa boku kwadratu, wiec interesujący nas stosunek promieni jest równy

a√ 2 R- --2-- √ -- r = a = 2 . 2
Wersja PDF