/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat/Udowodnij

Zadanie nr 6865832

Pole kwadratu 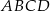ABCD jest równe 16. Punkt 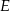E jest środkiem boku 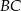BC , a punkt 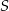S punktem przecięcia przekątnej 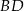BD kwadratu i odcinka 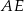AE . Wykaż, że odległość punktu 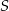S od boku 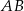AB jest równa 43 .

Wersja PDF

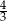Rozwiązanie

Rysujemy opisaną sytuację.

PIC

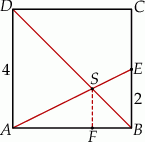
Zauważmy, że trójkąty 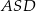ASD i ESB mają równe kąty, więc są podobne. Ponadto, skala ich podobieństwa jest równa

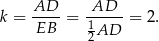
k = AD-- = AD----= 2. EB 1AD 2

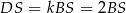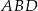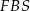To oznacza, że DS = kBS = 2BS i z podobieństwa trójkątów prostokątnych ABD i F BS (lub z twierdzenia Talesa) mamy

SF BS BS 1 DA 4 ----= ----= ---------- = -- ⇒ SF = ---- = --. DA DB 2BS + BS 3 3 3
Wersja PDF