/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat/Udowodnij

Zadanie nr 8160394

Na boku 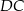DC kwadratu 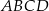ABCD obrano punkt 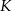K tak, że 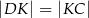|DK | = |KC | . Przekątna 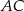AC kwadratu przecina odcinek 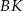BK w punkcie 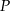P . Uzasadnij, że pole trójkąta 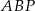ABP jest czterokrotnie większe niż pole trójkąta KCP .

PIC

Wersja PDF

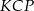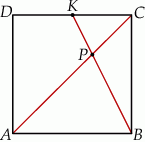
Rozwiązanie

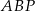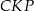Zauważmy, że trójkąty ABP i CKP mają równe kąty, więc są podobne. Ponadto, skala ich podobieństwa jest równa

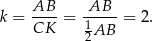
k = AB--= AB---= 2. CK 12AB

Ponieważ pole zmienia się jak kwadrat skali podobieństwa, mamy

PABP = k2PCKP = 4PCKP .
Wersja PDF