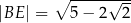/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat/Oblicz długość

Zadanie nr 3560553

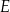Dany jest kwadrat ABCD o boku długości 2. Punkt E jest punktem przekątnej 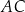AC , takim że 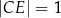|CE | = 1 . Oblicz długość odcinka BE .

Wersja PDF

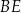Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

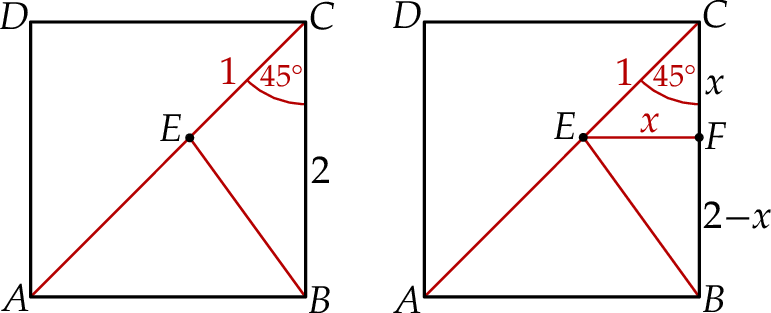
Sposób I

Stosujemy twierdzenie cosinusów w trójkącie 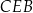CEB .

2 2 2 ∘ BE = CE + CB −-2CE ⋅CB cos45 √ 2 √ -- BE 2 = 1+ 4− 4 ⋅----= 5 − 2 2 ∘ ---------2 √ -- BE = 5− 2 2.

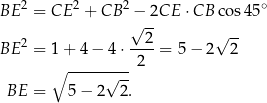
Sposób II

Dorysujmy odcinek 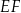EF równoległy do 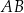AB i niech 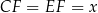CF = EF = x (trójkąt 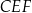CEF jest równoramienny). Mamy zatem

√ -- x2 + x2 = 1 ⇒ x2 = 1- ⇒ x = √1--= --2-. 2 2 2

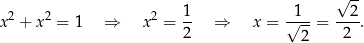
W takim razie 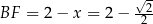√ - BF = 2− x = 2 − -22 i

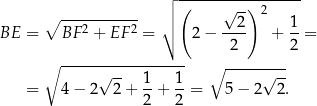
┌│ (-----√--)-2----- ∘ ----------- │∘ 2 1 BE = BF2 + EF 2 = 2− ---- + --= 2 2 ∘ -----√------------ ∘ -----√--- = 4− 2 2+ 1-+ 1-= 5 − 2 2. 2 2

 
Odpowiedź: ∘ -----√--- |BE | = 5 − 2 2

Wersja PDF