/Szkoła średnia/Liczby/Oś liczbowa/Przedziały

Zadanie nr 2103650

Dodaj do ulubionych
Dodaj do rozwiązanych

Na osi liczbowej zaznaczono przedział 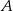A złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział 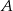A przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział 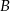B . Wyznacz wszystkie liczby całkowite, które należą jednocześnie do 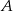A i do B .

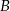Rozwiązanie

Zaznaczamy na osi przedziały 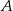A i B

PIC

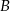
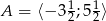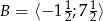Z obrazka widać, że A = ⟨− 312;512 ⟩ oraz B = ⟨− 112;7 12⟩ . W takim razie

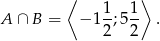
⟨ ⟩ A ∩ B = − 11;5 1- . 2 2

W przedziale tym jest 7 liczb całkowitych: -1,0,1,2,3,4,5.  
Odpowiedź: -1,0,1,2,3,4,5

Wersja PDF