Zadanie nr 2414065
Na rysunku przedstawiono kwadrat 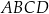 o polu 4.
o polu 4.

Punkty 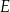 i
i 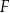 są środkami boków
są środkami boków 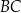 i
i 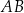 , a punkt
, a punkt 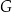 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 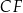 i
i 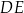 . Oblicz pole czworokąta
. Oblicz pole czworokąta 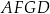
Rozwiązanie
Zauważmy, że trójkąty prostokątne 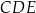 i
i 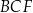 są przystające, więc możemy oznaczyć
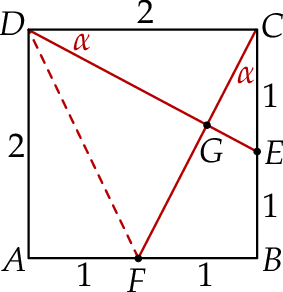
są przystające, więc możemy oznaczyć 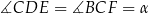 .
.
W trójkącie prostokątnym 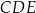 mamy ponadto
mamy ponadto
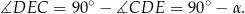
To oznacza, że trójkąt 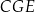 jest prostokątny, czyli odcinki
jest prostokątny, czyli odcinki 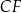 i
i 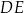 są prostopadłe.
są prostopadłe.
Zauważmy jeszcze, że
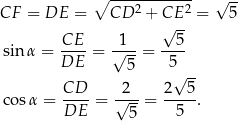
To pozwala nam obliczyć długości przyprostokątnych w trójkącie prostokątnym  .
.
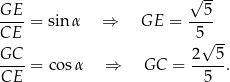
Sposób I
Pole czworokąta  możemy obliczyć jako sumę pól trójkątów
możemy obliczyć jako sumę pól trójkątów  i
i 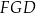 .
.
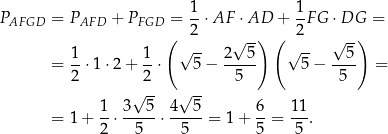
Sposób II
Tym razem obliczymy pole czworokąta 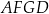 odejmując od pola kwadratu
odejmując od pola kwadratu 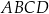 pola trójkątów
pola trójkątów 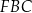 i
i 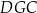 .
.
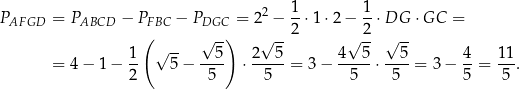
Odpowiedź: