Zadanie nr 3134178
Oblicz pole kwadratu wiedząc, że różnica pól kół opisanego i wpisanego w ten kwadrat jest równa 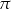 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
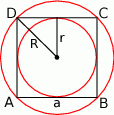
Jeżeli oznaczymy długość boku kwadratu przez  to promień okręgu wpisanego w kwadrat jest równy
to promień okręgu wpisanego w kwadrat jest równy 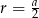 , a promień okręgu opisanego jest równy połowie długości przekątnej, czyli
, a promień okręgu opisanego jest równy połowie długości przekątnej, czyli 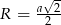 . Z podanej różnicy pól otrzymujemy równanie
. Z podanej różnicy pól otrzymujemy równanie
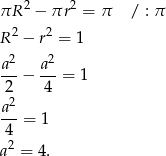
Odpowiedź: