/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat/Pole

Zadanie nr 5079808

Różnica między polem koła opisanego na kwadracie a polem koła wpisanego w kwadrat jest równa 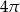4π . Oblicz pole kwadratu.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

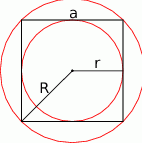
Widać na rysunku, że promień okręgu wpisanego w kwadrat jest równy połowie długości boku tego kwadratu. Natomiast promień okręgu opisanego na kwadracie jest równy połowie długości przekątnej. Zatem otrzymujemy

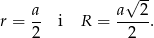
√ -- a a 2 r = -- i R = -----. 2 2

Z założeń otrzymujemy równanie

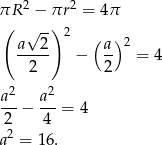
πR 2 − πr2 = 4π ( √ --) 2 a 2 ( a) 2 ----- − -- = 4 2 2 a2 a2 ---− ---= 4 2 4 a2 = 16.

Zatem pole kwadratu wynosi 16.  
Odpowiedź: 16

Wersja PDF