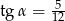Zadanie nr 9381165
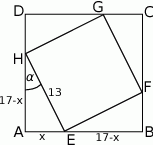
W kwadrat 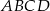 o boku długości 17 wpisano kwadrat
o boku długości 17 wpisano kwadrat 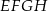 , jak pokazano na rysunku. Wiedząc, że przekątna kwadratu
, jak pokazano na rysunku. Wiedząc, że przekątna kwadratu 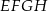 ma długość
ma długość 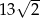 oblicz tangens kąta
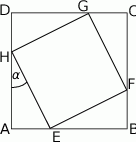
oblicz tangens kąta  zaznaczonego na rysunku.
zaznaczonego na rysunku.
Rozwiązanie
Skoro przekątna kwadratu 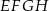 ma długość
ma długość 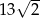 to jego bok musi mieć długość 13.
to jego bok musi mieć długość 13.
Oznaczmy 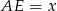 . Wtedy
. Wtedy 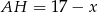 i z twierdzenia Pitagorasa w trójkącie
i z twierdzenia Pitagorasa w trójkącie 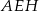 mamy
mamy
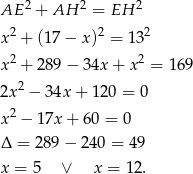
Z rysunku wnioskujemy, że 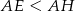 , więc
, więc 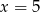 i szukany tangens jest równy
i szukany tangens jest równy
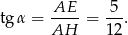
Odpowiedź: