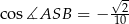Zadanie nr 1181119
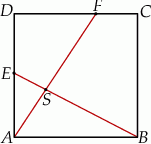
Na bokach  i
i  kwadratu
kwadratu  o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 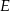 i
i 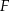 w ten sposób, że
w ten sposób, że 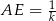 i
i 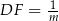 , dla
, dla 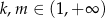 . Niech
. Niech 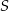 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 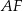 i
i 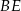
- Wykaż, że jeżeli trójkąt
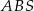 jest prostokątny to
jest prostokątny to 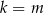 .
. - Oblicz cosinus kąta
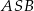 jeżeli
jeżeli 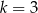 i
i 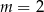 .
.
Rozwiązanie
- Ponieważ ani punkt
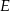 , ani
, ani 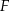 nie może być wierzchołkiem kwadratu, prosty musi być kąt
nie może być wierzchołkiem kwadratu, prosty musi być kąt 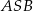 .
. 
Sposób I
Jeżeli oznaczymy
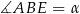 to mamy kolejno
to mamy kolejno 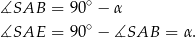
W takim razie trójkąty prostokątne
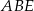 i
i 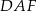 mają takie same kąty i
mają takie same kąty i 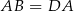 . W takim razie są przystające, czyli
. W takim razie są przystające, czyli 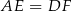 .
. Sposób II
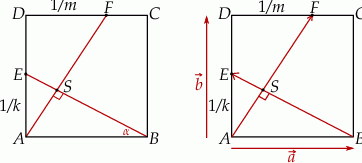
Zadanie możemy łatwo rozwiązać korzystając z iloczynu skalarnego. Jeżeli wprowadzimy na płaszczyźnie układ współrzędnych tak, aby
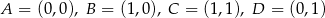
to
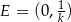 i
i 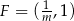 . Dalej
. Dalej ![[ ] → 1- AF = m ,1 → [ ] BE = − 1, 1- . k](https://img.zadania.info/zad/1181119/HzadR13x.gif)
Pozostało sprawdzić kiedy te wektory są prostopadłe.
![→ → [ ] [ ] 0 = AF ∘BE = 1-,1 ∘ − 1, 1 = − 1- + 1- ⇐ ⇒ k = m . m k m k](https://img.zadania.info/zad/1181119/HzadR14x.gif)
Sposób III
Rozwiązanie z poprzedniego sposobu można też zapisać bez układu współrzędnych. Jeżeli oznaczymy
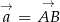 i
i 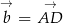 to mamy
to mamy 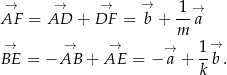
Teraz sprawdzamy kiedy iloczyn skalarny tych wektorów jest równy 0 (korzystamy z tego, że
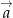 i
i 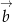 są prostopadłe i mają długość 1).
są prostopadłe i mają długość 1). 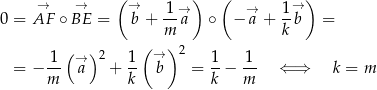
-
Sposób I
Oznaczmy
 i
i  .
. 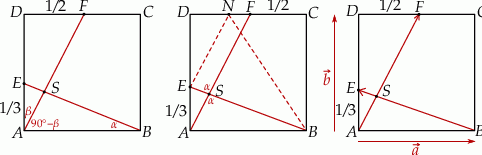
W takim razie mamy obliczyć
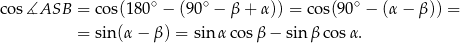
No i jest fajnie, bo te sinusy i cosinusy łatwo obliczyć z trójkątów prostokątnych
 i
i  . Mamy
. Mamy 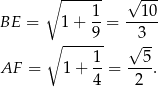
Stąd
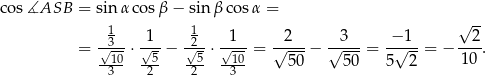
Sposób II
Jeżeli się uprzemy, to szukany cosinus możemy też obliczyć z twierdzenia cosinusów. Nie jest to jednak zupełnie natychmiastowe, bo nie za bardzo widać jak obliczyć długości boków trójkąta
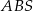 . Żeby ominąć ten problem, skorzystamy z innego trójkąta. Dorysujmy odcinek
. Żeby ominąć ten problem, skorzystamy z innego trójkąta. Dorysujmy odcinek 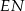 równoległy do odcinka
równoległy do odcinka 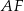 . Mamy
. Mamy 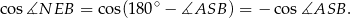
W takim razie wystarczy obliczyć cosinus kąta przy wierzchołku
 w trójkącie
w trójkącie  i wynik pomnożyć przez
i wynik pomnożyć przez  .
. Teraz cała zabawa polega na tym, że długości boków trójkąta
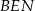 są dość proste do obliczenia. Zauważmy, że
są dość proste do obliczenia. Zauważmy, że 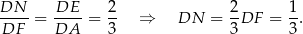
Mamy więc
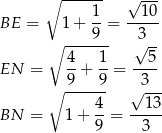
Pozostało teraz napisać twierdzenie cosinusów.
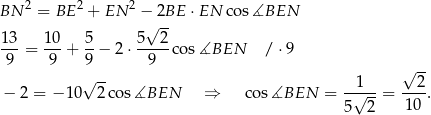
Na koniec musimy sobie przypomnieć, że mieliśmy przemnożyć wynik przez
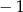 .
. Sposób III
Jedno z rozwiązań w podpunkcie a) polegało na wprowadzeniu na płaszczyźnie układu współrzędnych. Możemy wykorzystać obliczone tam wektory
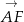 i
i 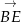 i skorzystać ze wzoru na cosinus kąta między wektorami.
i skorzystać ze wzoru na cosinus kąta między wektorami. ![[ ] A→F = 1,1 2 → [ ] BE = − 1 , 1- 3 → → 1 1 1 √ -- co s∡ ( →AF ,B→E ) =-AF-∘-BE--= ∘---−-2-+∘-3-----= −√-6-= -−√-1-= − --2. → → 1 1 --50- 5 2 10 |AF ||BE | 4 + 1 1 + 9 6](https://img.zadania.info/zad/1181119/HzadR43x.gif)
Sposób IV
Możemy też obliczyć szukany cosinus używając wektorów bez układu współrzędnych. Ponownie korzystamy ze wzorów wyprowadzonych w podpunkcie a). Mamy
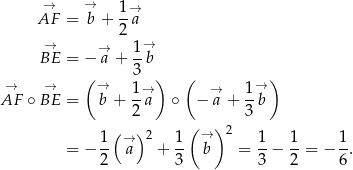
Mamy stąd
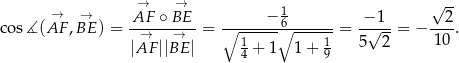
Odpowiedź: