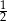Zadanie nr 3065127
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości stożka do objętości walca wynosi 8 : 3. Oblicz tangens kąta zawartego między wysokością a tworzącą stożka.
Rozwiązanie
Rysujemy przekrój osiowy opisanej sytuacji.
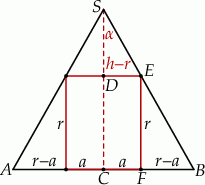
Niech  i
i 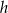 będą długościami promienia podstawy i wysokości stożka, a przez
będą długościami promienia podstawy i wysokości stożka, a przez  oznaczmy promień podstawy walca. Dany stosunek objętości daje nam warunek
oznaczmy promień podstawy walca. Dany stosunek objętości daje nam warunek
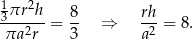
Musimy jeszcze wykorzystać to, że walec jest wpisany w stożek – mamy stąd podobieństwo trójkątów 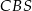 i
i 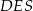 . Stąd
. Stąd
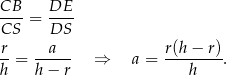
Wstawiamy to do poprzedniej równości.
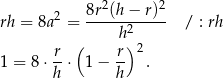
Podstawmy teraz 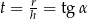 .
.
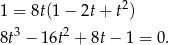
Szukamy teraz pierwiastka wymiernego, można znaleźć 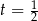 . Dzielimy teraz wielomian przez
. Dzielimy teraz wielomian przez 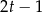 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
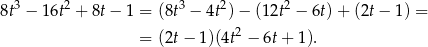
Teraz rozkładamy trójmian w nawiasie.
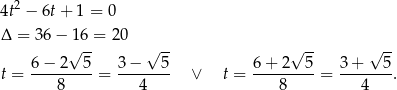
Aby wybrać właściwe pierwiastki zauważmy, że przy naszych oznaczeniach musi być 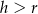 , czyli
, czyli 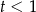 . Zatem
. Zatem 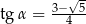 lub
lub 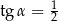 .
.
Odpowiedź: 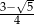 lub
lub