/Szkoła średnia/Geometria/Stereometria/Stożek/Kąt

Zadanie nr 9609892

Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.

Wersja PDF

Rozwiązanie

Rozpoczynamy od rysunku, od razu skupiamy się na przekroju osiowym.

PIC

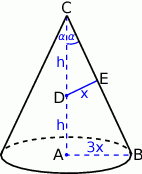
Niech 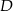D będzie środkiem wysokości i powiedzmy, że dzieli on wysokość na odcinki długości 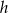h . Oznaczmy też przez x odległość tego punktu od powierzchni bocznej stożka.

Sposób I

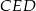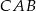Zauważmy, że trójkąty CED i CAB są prostokątne i mają wspólny kąt przy wierzchołku 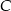C . Są więc podobne. Mamy więc

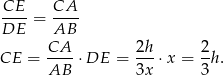
CE-- CA-- DE = AB CA 2h 2 CE = ----⋅DE = ---⋅x = -h . AB 3x 3

Piszemy teraz twierdzenie Pitagorasa w trójkącie 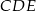CDE .

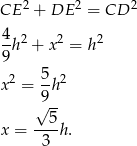
CE 2 + DE 2 = CD 2 4h2 + x2 = h2 9 2 5 2 x = --h √9-- x = --5-h. 3

Mamy zatem

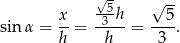
√5- √ -- sin α = x-= -3 h-= --5-. h h 3

To jednak nie koniec, bo mamy wyliczyć 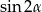sin2α , a nie 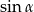sin α . Aby móc skorzystać ze wzoru

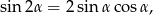
sin 2α = 2 sinα cos α,

wyliczymy jeszcze 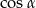cosα .

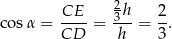
CE 23h 2 cos α = CD-- = h--= 3.

Mamy więc

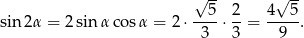
√ -- √ -- 5 2 4 5 sin2 α = 2 sin α cosα = 2⋅ ---⋅ --= ----. 3 3 9

Sposób II

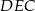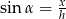Z trójkąta prostokątnego DEC mamy sin α = xh , a trójkąt prostokątnego 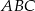ABC mamy

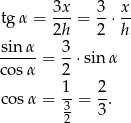
3x 3 x tg α = --- = --⋅ -- 2h 2 h sin-α = 3⋅ sin α cos α 2 1- 2- co sα = 3 = 3 . 2

W takim razie, korzystając z jedynki trygonometrycznej mamy

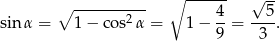
∘ ---------- ∘ ------ √ -- sin α = 1 − cos2α = 1 − 4-= --5-. 9 3

Stąd

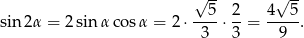
√ -- √ -- sin2 α = 2 sin α cosα = 2⋅ --5⋅ 2-= 4--5. 3 3 9

 
Odpowiedź: √ - 4--5 9

Wersja PDF