Zadanie nr 5983392
Ze zbioru 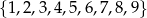 wybieramy jedną liczbę, a potem jeszcze jedną większą od niej. Na ile sposobów możemy to zrobić?
wybieramy jedną liczbę, a potem jeszcze jedną większą od niej. Na ile sposobów możemy to zrobić?
A) 72 B) 36 C) 81 D) 17
Rozwiązanie
Sposób I
Wypisujemy wszystkie pary spełniające warunki zadania.

Jest więc
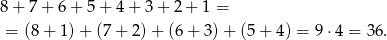
możliwości.
Sposób II
Parę 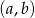 różnych liczb z danego zbioru możemy wybrać na
różnych liczb z danego zbioru możemy wybrać na
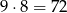
sposoby (pierwszą liczbę możemy wybrać na 9 sposobów, a drugą na 8 sposobów). To jednak nie jest dokładnie to, co mieliśmy obliczyć, bo np. pary 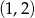 i
i 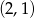 dają ten sam wybór liczb spełniających nierówność
dają ten sam wybór liczb spełniających nierówność 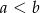 . Musimy więc obliczoną wyżej liczbę par podzielić przez 2 i jest
. Musimy więc obliczoną wyżej liczbę par podzielić przez 2 i jest
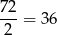
możliwych wyborów.
Sposób III
Pytanie z treści zadania sprowadza się do pytania ile par różnych liczb można wybrać z danego zbioru. Jest ich więc
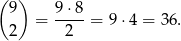
Odpowiedź: B

